Спад і втрата напруги в мережах змінного струму

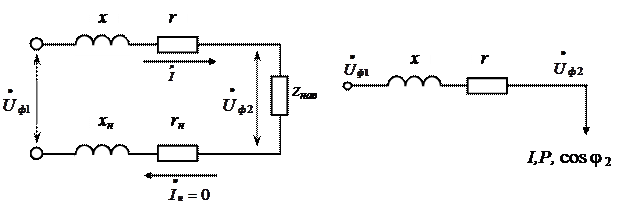
Розглянемо лінію трифазного змінного струму із навантаженням в кінці (рисунок 6.2, а). Вважатимемо, що навантаження усіх трьох фаз однакові. В цьому випадку трифазну лінію можна зобразити у вигляді однієї лінії (рисунок 6.2, б) і вести розрахунок для фазних напруг та струмів а потім перейти до їх лінійних значень.

а б

а – розгорнута схема; б – однолінійна схема

Рисунок 6.2 – Одна фаза лінії трифазного струму із симетричним навантаженням на кінці

На рисунку 6.2 прийняті наступні позначення: та – фазна напруга, відповідно, на початку і в кінці лінії; 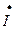– струм навантаження,

соs j ₂ – коефіцієнт потужності навантаження, r – активний опір проводу, х – індуктивний опір проводу, z _нав – повний опір навантаження.

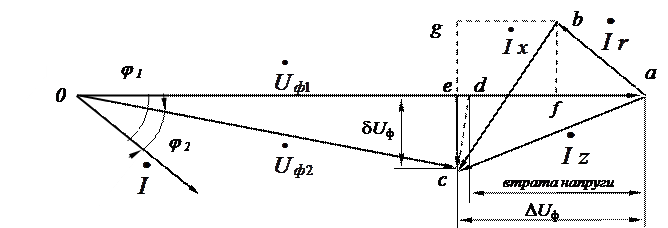Струм, що проходить по провіднику, створює в ньому падіння (спад) напруги. Тому напруга в кінці лінії відрізняється від напруги на її початку. Вектор падіння напруги в активному опорі збігається за напрямом із вектором струму, а вектор падіння напруги в індуктивному опорі випереджає вектор струму на 90⁰. Тому, в загальному випадку, вектор напруги в кінці лінії відрізняється від вектора напруги на початку лінії не лише за значенням, а й за напрямом. Для запропонованої схеми побудуємо векторну діаграму (рисунок 6.3).

Рисунок 6.3 – Векторна діаграма для однієї фази трифазної лінії із навантаженням на кінці

Відкладаємо вектор напруги на початку лінії 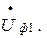Під кутом j ₁ до нього відкладаємо вектор струму 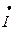. Щоб отримати вектор напруги в кінці лінії 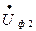необхідно від напруги на початку лінії відняти падіння напруги в ній:

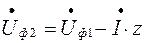. (6.16)

Для цього з кінця вектора напруги 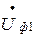(0 a) паралельно вектору струму 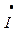, але в протилежному напрямку відкласти вектор спаду напруги в активному опорі 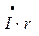(a b), а під кутом 90⁰ до нього відкласти вектор спаду напруги в реактивному опорі 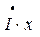(b c). Вектор 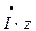(а с) і буде падінням напруги в повному опорі магістралі. Сполучивши точку 0 з точкою с отримаємо вектор напруги в кінці лінії (0 с).

Геометрична різниця між вектором напруги на початку і в кінці лінії називається падінням напруги:

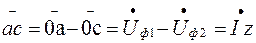. (6.17)

Якщо в напрямку вектора 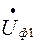(0 a) відкласти значення вектора

напруги в кінці лінії 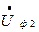(0 d), то матимемо відрізок a d – алгебрагічну різницю. Алгебрагічну різницю між напругою на початку лінії і в кінці називають втратою напруги:

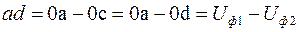. (6.18)

Падіння (спад) напруги можна розглядати не лише як суму його активної і реактивної складових. Опустивши із точки с перпендикуляр на напрямок вектора 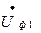(0 a), із трикутника а-е-с матимемо:

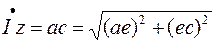. (6.19)

Відрізок а е називають поздовжньою складовою падіння напруги
і позначають .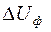

Відрізок е с називають поперечною складовою падіння напруги і позначають .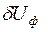

Опустивши перпендикуляр з точки b на вектор (0 a), і побудувавши прямокутник e g b f (рисунок 6.3), матимемо:

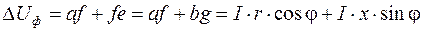. (6.20)

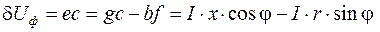. (6.21)

Міжфазна складова напруги більша від фазної в 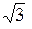рази, тому для поздовжньої складової міжфазної (лінійної) напруги можна записати:

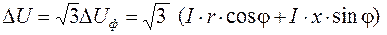, (6.22)

а для поперечної складової міжфазної (лінійної) напруги:

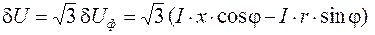, (6.23)

або

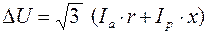, (6.24)

. (6.25)

Якщо навантаження задано у вигляді потужності, тоді:

; ; .

Увівши значення потужності в рівняння (6.24) та (6.25), матимемо:

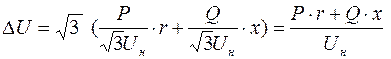, (6.26)

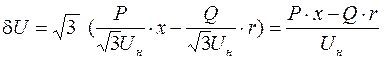. (6.27)

Якщо магістраль живить кількох споживачів, то рівняння (6.24) та (6.25) приймуть вигляд:

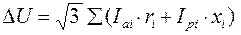, (6.28)

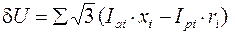, (6.29)

а рівняння (6.26) та (6.27) приймуть, відповідно, наступний вигляд:

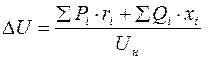; (6.30)

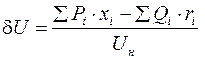. (6.31)

Для споживачів значення має не фаза, а абсолютне значення напруги, тому мережі розраховують не за падінням, а за втратою напруги.

З трикутника 0 е с (рисунок 6.3) можна записати, що

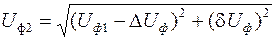. (6.32)

Втрата напруги:

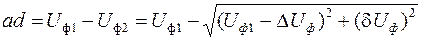. (6.33)

Якщо відома напруга в кінці ділянки 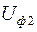, то знаючи падіння напруги на ділянці можна знайти напругу на початку ділянки 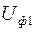. Вона дорівнює геометричній сумі напруги в кінці ділянки і падіння напруги на ній:

. (6.34)

Втрату напруги можна визначити аналогічно рівнянню (6.33):

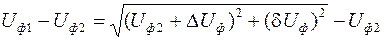(6.35)

З векторної діаграми (рисунок 6.3) видно, що за значенням втрата напруги відрізняється від поздовжньої складової спаду напруги на незначний за довжиною відрізок e d. Тому, для практичних розрахунків, в електричних мережах напругою до 35 кВ включно втрату напруги прирівнюють поздовжній складовій падіння напруги:

. (6.36)

Похибка від такого припущення не перебільшує 5 %.

Лінійна втрата напруги при цьому, якщо j ₂ = j, дорівнює:

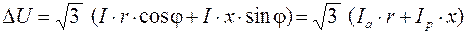, (6.37)

або

. (6.38)

Дата добавления: 2013-12-13