Арифметические алгоритмы и их применение в криптографии

Лекция_4_часть_2.

Литература

1. Голосенко И.А., Козловский В.В. История русской социологии XIX-XX веков. – М., 1995.

2. М.М. Ковалевский в истории российской социологии и общественной мысли./Под ред. А.О. Бороноева. – СПб., 1996.

3. Социология в России./Под ред. В.А. Ядова. – М., 1998.

4. Проблемы теоретической социологии./Под ред. А.О. Бороноева. – СПб., 1994.

5. Клементьева Д.С., Панкова Л.Н. Антология русской классической социологии. – М., 1996.

6. Немировский В.Г. Современная теоретическая социология. Учеб. пособие./ В.Г. Немировский; Краснояр. гос. ун-т. – Красноярск, 2003.

7. Социология: Учебник./Под ред. Д.В. Иванова. – М., 2005.

8. Меморандум III Всероссийского социологического конгресса.//Социс. 2009. № 3.

9. Осипов Г.В. Отечественная социология: история и современность.//Социс. 2009. № 3.

10. Лавров П.Л. Философия и социология.//Избранные произведения. В 2-х т. – М.,1965.

11. Волков Ю.Г., Мостовая И.В. Социология в вопросах и ответах: Учебное пособие. – М.: Гардарики, 1999. Вопросы 9-13.

* Чаще всего в исторической литературе по социологии используют только первую часть фамилии этого автора – Богданов А.А.

* Квази от лат. quasi – якобы, как будто.

Натуральное число p, больше единицы называется простым, если оно делится нацело только на 1 и на себя.

Теорема (Эвклид). Множество простых чисел бесконечно.

Обозначим через p(x) функцию, которая равна числу простых чисел p в интервале 1 < x <p. Российский математик П. Л. Чебышев в 1850г. показал [7], что 0,921

x / ln x < p(x) < 1,106 x / ln x.

Простые числа являются важным понятием в криптографии. Многие современные криптографические системы строятся на базе простого числа. Поэтому алгоритмы генерации простых чисел и проверки на простоту сформированного числа являются важными инструментами при создании криптографической системы.

Простые числа встречаются довольно часто.

Заметим, что существует около 10151 простых чисел длиной от 1 до 512 бит включительно [10], а количество простых чисел меньших 2512 приблизительно равно 2503/ Для чисел близких n вероятность произвольно выбранному числу оказаться простым числом, равна 1/ln(n). При случайном выборе двух простых чисел в диапазоне от 1 до 151 бита вероятность совпадения этих чисел ничтожно мала. Простые числа играют

важную роль в современной криптографии. Многие современные криптографические системы с открытыми (или не симметричными) ключами формируются с применением простых чисел.

Для простых чисел будем рассматривать три задачи:

· построение простых чисел;

· проверка чисел на простоту;

· факторизация (разложения) чисел на простые множители.

На самом деле все эти три задачи фактически дают ответ на один вопрос: является ли рассматриваемое число простым. Но для каждой из этих задач применяются свои методы. Для первой задачи, используя необходимые условия простоты, можно давать ответы типа:

· заданное число n не простое;

· вероятность того, что заданное число n не простое, меньше заданного числа e.

Для второй задачи можно строить некоторую последовательность чисел специального вида. И для чисел данной последовательности применять некоторые тесты до тех пор, пока не найдем среди них простое число.

Приведем некоторые определения, теоремы, алгоритмы, которые связаны с вопросами решения

поставленных задач

Определение 1. Числа Fk = 2a + 1, a = 2k, k = 0, 1, 2, …, называются числами Ферма.

Теорема 1. Число Ферма n = Fk при k > 0 является

простым тогда и только тогда, когда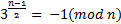

Определение 2. Пусть p – простое число. Числа вида Mp = 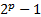называются числами Мерсенна.

Интерес к числам Мерсенна вызван их связью с так называемыми совершенными числами — числами, равными сумме всех своих делителей, отличных, конечно, от самого числа. Ещё Евклид доказал (докажите и вы), что если простое число p имеет вид Mp, то число p(p+1)/2 является совершенным. Например,

3 = 2² – 1, 7 = 2³ – 1

простые числа, и соответственно

6 =	(3·4)/2 = 1 + 2 + 3,
28 =	(7·8)/2 = 1 + 2 + 4 + 7 + 14

, где Mp является числом Мерсенна. Напомним, совершенным числом называется число, которое равно сумме всех своих делителей, меньших, чем оно само.

Числа Мерсенна редки. В 2001году было найдено тридцать девятое число Мерсенна для p = 1 3466 917.

Для проверки простоты чисел Мерсенна применяется следующая теорема [7].

Теорема 2. Пусть p – простое число, p > 2, Mp =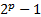

1. Рассмотрим последовательность L0, L1, …, которая

определяется соотношениями

L0 = 4, 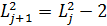mod p, 0 ≤ j < p.

Число Mn – простое тогда и только тогда, когда Lq-2 =0 mod p.

Дата добавления: 2013-12-13