Теорема Лагранжа – Дирихле

Теорема устанавливает достаточные условия устойчивости равновесия.

Теорема. Для устойчивости положения равновесия консервативной системы с голономными, идеальными, стационарными и удерживающими связями достаточно, чтобы потенциальная энергия в положении равновесия имела минимум П = П_min .

Выберем область значений обобщенных координат вблизи положения равновесия.

- наперед заданное число, так, чтобы внутри и на границе этой области выполнялось условие

П > П_min при .

Выбранная область значения q_i называется областью минимума функции. Рассмотрим значение П, когда одна из координат q_i находится на границе области минимума, т.е.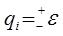

Наибольшее среднее этих значений > П_min.

Обозначим это наименьшее значение + λ, где λ > 0. Т.о. если хотя бы одна из обобщенных координат находится на границе области минимума, то

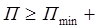λ. (1)

Выведем систему из начального положения равновесия, сообщив таким системам достаточно малые возмущения, которым соответствуют обобщенные координаты q_i из области минимума и достаточно малые скорости. Т.к. система находится под действием консервативных сил, то к ней применим закон сохранения полной механической энергии

Т + П = Т_о + П_о; (2)

Т _о и П _о для t =0.

Т является неотрицательной величиной, поэтому из (2) следует

(3)

Выберем такие малые начальные возмущения (начальные отклонения 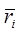и начальной скорости 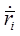) и соответствующие им значения обобщенных координати обобщенных скоростей настолько малыми, чтобы:

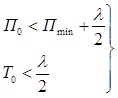(4)

Это всегда возможно, т.к. П является непрерывной функцией обобщенных координат 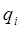, а кинетическая энергия Т непрерывной функцие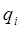й и .

Из (3) и (4) ® П < П_min + λ.

Т.е. данное положение – равновесие, в котором П = П_min есть положение устойчивого равновесия (обобщенные координаты 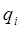остаются внутри области минимума (), т.е. система не стремиться к дальнейшему увеличению отклонения от положения равновесия).

В этом случае 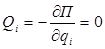, т.е. П достигает экстремума (max или min).

Дата добавления: 2013-12-13