Гармонические колебания

Среди разнообразных периодических движений особое место занимает гармоническое колебательное движение. Гармоническими называют колебания, в которых интересующая нас величина х (например, линейное или угловое смещение из положения равновесия, скорость, ускорение, заряд, напряжение и т.д.) изменяется со временем t по закону косинуса или синуса, то есть

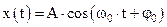, (1)

или

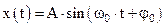
Здесь:

- А – амплитуда (максимальное значение величины х). Определяется начальными условиями. Измеряется в единицах величины х.

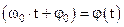- – фаза колебания. Определяет мгновенное значение величины х в момент времени t. За период фаза получает приращение .

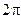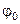- – начальная фаза колебания. Определяется значением величины х в момент времени t=0.

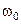- – собственная циклическая (круговая) частота колебаний. Определяется параметрами колебательной системы. Измеряется в .

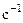Циклическая частота связана с линейной частотой и периодом следующими соотношениями .

Скорость и ускорение тела также изменяются по гармоническому закону. Продифференцировав по времени уравнение (1) найдем скорость изменения величины х — 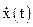и ускорение :

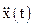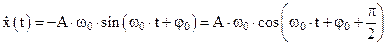
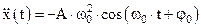. (2)

При этом максимальное значение скорости колеблющегося тела V_max = Aω₀, максимальное значение модуля ускорения a_{max =} Aω₀².

Кинетическая энергия колеблющегося тела W_k = ½mv² = ½mA²ω₀² sin² (ω₀t+φ).

Потенциальная энергия (учитывая, что сила квазиупругая) W_п = ½ kx² = ½ kA² cos² (ω₀t+φ).

Полная энергия системы при гармонических колебаниях W= W_k + W_п =½ kA² = ½ mω₀² A².

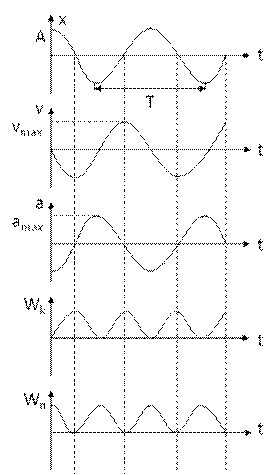
На рисунке приведены графики зависимости от времени смещения х, скорости V, ускорения а, кинетической W_k и потенциальной W_п энергии гармонических колебаний при начальной фазе φ = 0. Из рисунка видно, частота изменения кинетической W_k и потенциальной W_п энергии при гармонических колебаниях вдвое больше частоты изменения смещения, скорости и ускорения.

Сопоставив уравнения (1) и (2), видим, что 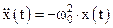, или

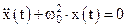. (3)

Это линейное однородное дифференциальное уравнение второго порядка называют уравнением гармонических колебаний.

Колебательная система, совершающая гармонические колебания, называется гармоническим осциллятором. Если колебательная система, совершающая гармонические колебания, обладает одной степенью свободы (для характеристики положения достаточно одной координаты), то такая система называется линейным гармоническим осциллятором.

Для определения характера движения механической системы составляют уравнение движения системы (исходя из законов динамики или закона сохранения энергии). Если уравнение при этом приводится к виду (3), то можно однозначно утверждать, что данная система совершает гармоническое колебание, собственная частота 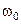которого равна корню квадратному из коэффициента при х(t). Воспользуемся этим методом для определения циклических частот и периодов колебаний пружинного и математического маятников.

Рассмотрим сначала пружинный маятник (рис 1 б). Пусть подвешенное к пружине тело оттянуто от положения равновесия на расстояние х (рис.1.в), а затем предоставлено самому себе. На тело действуют сила тяжести и сила упругости. Под действием этих сил тело движется с ускорением. Запишем уравнение второго закона Ньютона для этого случая (рис.1.в)

.

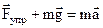Это уравнение в проекции на ось ОХ и с учетом того, что для одномерного движения ускорение – это вторая производная от координаты по времени, то есть 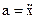, запишется

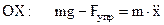. (4)

Величину силы упругости 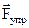, действующей на тело массой m, найдем по формуле закона Гука

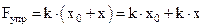. (5)

После подстановки (5) в (4) получим

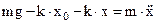(6)

Величину растяжения пружины в положении равновесия 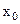(рис.1.а и 1.б) найдем из уравнения второго закона Ньютона для неподвижного тела, подвешенного к пружине ,

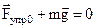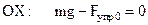, (7)

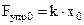, (8)

Из (7) и (8) следует, что

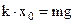. (9)

После подстановки (9) в (6) и приведения подобных слагаемых получаем: 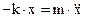, или

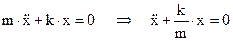(10)

Сравнив уравнения (3) и (10), получим, что для пружинного маятника . .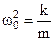

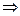
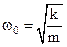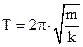(11)

Похожие рассуждения можно провести для математического маятника (рис.2) и показать, что . .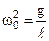

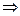
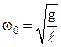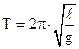(12)

Математический маятник – это материальная точка на невесомой и нерастяжимой нити длиной. При гармонических колебаниях смещение маятника от положения равновесия х много меньше длины нити х << 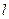, поэтому для угла отклонения нити от вертикали 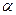имеет место соотношение

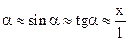
Следовательно, второй закон Ньютона для материальной точки массы m: ma = F можно записать в виде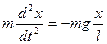, где - ускорение точки, F = mg sin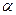=mg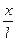- возвращающая сила. Знак минус в правой части означает, что возвращающая сила направлена противоположно смещению х.

Таким образом, дифференциальное уравнение гармонических колебаний математического маятника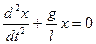

Получаем период колебаний математического маятника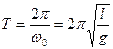

Физический маятник – это абсолютно твёрдое тело, совершающее колебания относительно горизонтальной оси О, не проходящей через центр масс маятника С. Основное уравнение динамики вращательного движения для маятника Jε = M, где J – момент инерции маятника относительно горизонтальной оси проходящей через точку О. Угловое ускорение маятника ε 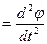. Момент силы тяжести маятника относительно горизонтальной оси, проходящей через точку О M = mgd sinφ, где m – масса маятника, d = CO – расстояние от оси до центра масс маятника С. При малых углах отклонения маятника от вертикали можно считать, что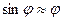

Подставляя (2.22), (2.23) с учётом (2.24) в выражение (2.21), получаем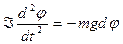

Минус означает, что момент возвращающей силы противоположен угловому перемещению. Отсюда получаем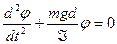

Это дифференциальное уравнение гармонических колебаний физического маятника. Из сравнения (2.26) и (2.7), находим период колебаний физического маятника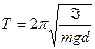

Сопоставляя (2.27) и (2.20), находим приведенную длину физического маятника 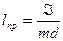, 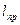- это длина нити математического маятника, у которого период колебаний совпадает с периодом данного физического маятника.

Колебания называются собственными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Дата добавления: 2013-12-13