Затухающие колебания

Все реальные колебательные системы являются диссипативными[1]. Энергия механических колебаний системы с течением времени расходуется на работу против сил трения, поэтому собственные колебания всегда затухают – их амплитуда постепенно уменьшается. Потеря энергии происходит и при деформациях тел, так как вполне упругих тел не существует, а деформации не вполне упругих тел сопровождаются частичным переходом механической энергии в энергию хаотического теплового движения частиц этих тел.

Во многих случаях в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаний, пропорциональны величине скорости. Будем называть эти силы, независимо от их происхождения, силами трения или сопротивления и вычислять их по следующей формуле: . Здесь r – коэффициент сопротивления среды, 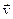– скорость движения тела. Знак минус указывает на то, что силы трения всегда направлены в сторону, противоположную направлению движения тела.

Запишем уравнение второго закона Ньютона для затухающих прямолинейных колебаний пружинного маятника

. (13)

Здесь: m – масса груза, k – жесткость пружины, 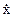– проекция скорости на ось ОХ, 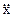– проекция ускорения на ось ОХ. Поделим обе части уравнения (13) на массу m и перепишем его в виде:

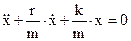. (14)

Введем обозначения:

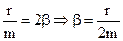, (15)

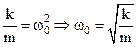. (16)

Назовем коэффициентом затухания, а 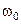мы ранее назвали собственной циклической частотой. С учетом введенных обозначений (15 и 16) уравнение (14) запишется

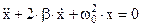. (17)

Это дифференциальное уравнение затухающих колебаний любой природы. Вид решения этого линейного дифференциального уравнения второго порядка зависит от соотношения между величиной 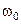– собственной частотой незатухающих колебаний и коэффициентом затухания .

Если трение очень велико (в этом случае 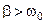), то система, выведенная из положения равновесия, возвращается в него, не совершая колебаний («ползет»). Такое движение (кривая 2 на рис.3) называют апериодическим.

Если же в начальный момент система с большим трением 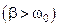находится в положении равновесия и ей сообщается некоторая начальная скорость 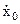, то система достигает наибольшего отклонения от положения равновесия 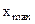, останавливается и после этого смещение асимптотически стремится к нулю (рис.4).

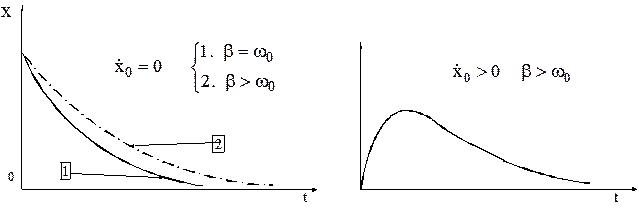Рис.3 Рис.4

Если система выведена из положения равновесия при условии 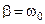и отпущена без начальной скорости, то система также не переходит положения равновесия. Но в этом случае время практического приближения к нему оказывается меньше, чем в случае большого 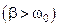трения (кривая 1 на рис 3). Такой режим называется критическим и к нему стремятся при использовании различных измерительных приборов (для быстрейшего отсчета показаний).

при малом трении (в этом случае ) движение носит колебательный характер (рис.5) и решение уравнения (17) имеет вид:

. (18)

Формула

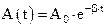(19)

описывает изменение амплитуды затухающих колебаний со временем. Амплитуда затухающих колебаний уменьшается с течением времени (рис.5) и тем быстрее, чем больше коэффициент сопротивления и чем меньше масса колеблющегося тела, то есть чем меньше инертность системы.

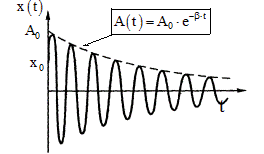Рис.5

Величину

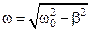(20)

называют циклической частотой затухающих колебаний. Затухающие колебания представляют собой непериодические колебания, так как в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Поэтому назвать 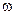частотой можно лишь условно в том смысле, что она показывает, сколько раз за секунд колеблющаяся система проходит через положение равновесия. По этой же причине величину

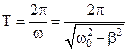(21)

можно назвать условным периодом затухающих колебаний.

Для характеристики затухания введем следующие величины:

- логарифмический декремент затухания;

- время релаксации;

- добротность.

Отношение двух любых последовательных смещений, разделенных во времени одним периодом называют декрементом затухания.

Логарифмическим декрементом затухания 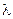называется натуральный логарифм отношения значений амплитуды затухающих колебаний в моменты времени t и t+T (натуральный логарифм отношение двух любых последовательных смещений, разделенных во времени одним периодом):

.

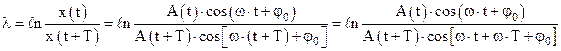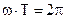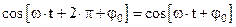Поскольку и , то .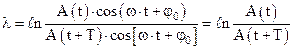

Воспользуемся формулой зависимости амплитуды от времени (19) и получим

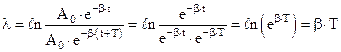(22)

Выясним физический смысл величин и 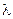. Обозначим через 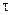промежуток времени, за который амплитуда затухающих колебаний убывает в е раз и назовем его временем релаксации. Тогда . отсюда следует, что

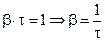. (23)

Следовательно, коэффициент затухания есть физическая величина обратная времени релаксации. Пусть N_e – число колебаний, за которое амплитуда затухающих колебаний убывает в е раз. Тогда

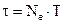. (24)

Из формул (22), (23) и (24) получим

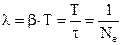. (25)

Следовательно, логарифмический декремент затухания 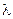есть физическая величина обратная числу колебаний, по истечении которых амплитуда затухающих колебаний убывает в е раз.

Добротностью колебательной системы 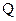назовем отношение

. (26)

Из формул (25) и (26) следует, что 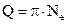. Это означает, что добротность пропорциональна числу колебаний, совершаемых системой за время релаксации.

Если затухание мало, то добротность можно определить следующим образом: 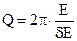. Здесь Е – полный запас энергии в одном из положений наибольшего отклонения, 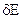– потери энергии за период. Добротность определяет относительную убыль энергии за период, подобно тому, как декремент – относительную убыль амплитуды.

Дата добавления: 2013-12-13