
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Первый замечательный предел. Тема. Первый и второй замечательные пределы
|
|
|
|
Лекция № 8, ВАС-11, 1 сем, 2012
Тема. Первый и второй замечательные пределы. Число e. Натуральный логарифм. Эквивалентные бесконечно малые функции.
В математике и ее приложения большую роль играет предел, который имеет вид:
 . (1.1)
. (1.1)
Этот предел носит название: первый замечательный предел. (Заметим, аргумент синуса измеряется в радианах, но не в градусах!!!). Докажем этот предел.
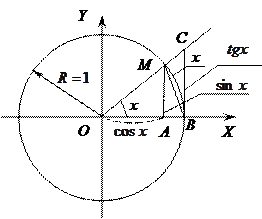 Возьмем круг радиуса
Возьмем круг радиуса 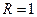 , обозначим радианную меру угла MOB через х (рис. 1.1). Так как радиус круга равен единице, то длина дуги
, обозначим радианную меру угла MOB через х (рис. 1.1). Так как радиус круга равен единице, то длина дуги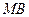 равна
равна 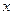 ,
, 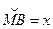 .
.
Рис. 1.1
Проведем доказательство для случая 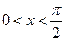 , т.е. предпольем, что угол
, т.е. предпольем, что угол 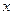 находится в первом квадранте. На рис. 1.1
находится в первом квадранте. На рис. 1.1 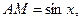
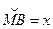 ,
, 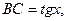
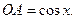 Очевидно, имеем:
Очевидно, имеем:
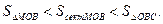 (1.2)
(1.2)
Величины площадей равны:
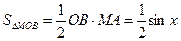 ,
, 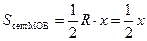 ,
,
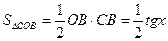 .
.
Подставим величины площадей в двойное неравенство (1.2):
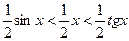
Разделим последнее неравенства на 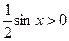 , получим:
, получим:
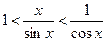 ,
,
или
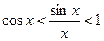 ,
,
но 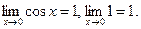 Отсюда следует:
Отсюда следует:
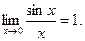
Мы доказали первый замечательный предел в предположении того, что 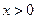 . Не представляет труда доказать его и для случая
. Не представляет труда доказать его и для случая 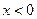 .
.
С помощью калькулятора можно убедиться в справедливости равенства 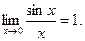 Для этого вычислим отношение
Для этого вычислим отношение 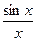 для различных значений
для различных значений 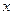 , уменьшая величину
, уменьшая величину 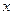 .
.
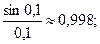
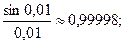
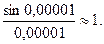
Из первого замечательного вытекает ряд следствий:
10. 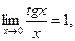 20.
20. 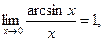 30.
30. 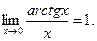 (1.3)
(1.3)
Докажем первое следствие. Второе и третье следствия примем без доказательства.
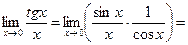
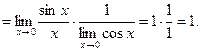
Проиллюстрируем применение первого замечательного предела для раскрытия неопределенности.
Задача 1.1. Найти предел функций:
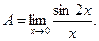
Решение. Имеем неопределенность вида:
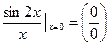 .
.
Для раскрытия неопределенности преобразуем функцию, умножим на 2 числитель и знаменатель дроби:
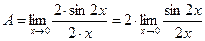 .
.
Введем новую переменную 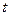 по формуле
по формуле 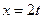 . Очевидно,
. Очевидно, 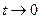 при
при 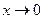 . Отсюда получаем:
. Отсюда получаем:
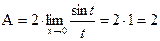 .
.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 612; Нарушение авторских прав?; Мы поможем в написании вашей работы!