Оценка точности метода наименьших квадратов

Пример 1

Литература

1. Всемирный историко-педагогический процесс: концепции, модели, историография. – М., 1996.

2. Джуринский А.Н. История образования и педагогической мысли. Учебник для студ. Высших учеб. заведений. - М.: Владос-Пресс, 2006. - 400 с.

3. История образования и педагогической мысли за рубежом и в России. Учеб. пособие для студентов высших пед. учебных заведений. / Под ред. З.И. Васильевой. - М.: ИЦ «Академия», 2005. - 416 с.

4. История педагогики и образования. От зарождения воспитания в первобытном обществе до конца ХХ века. Учеб. пособие для пед. учеб. заведений. / Под ред. А.И. Пискунова. - М.: ТЦ «Сфера», 2006. - 496 с.

5. Кувырталова М.А. История образования и педагогической мысли: Учебно-методическое пособие для студентов педагогических специальностей ВУЗов / М.А. Кувырталова, Э.В. Власов, Ю.А. Тарасова. – Тула: Изд-во Тул. гос. пед. ун-та им. Л.Н. Толстого, 2006 – 333 с.

6. Педагогический энциклопедический словарь. – М., 2003.

7. Российская педагогическая энциклопедия. – В 2-х т. – Т. 1. – М., 1993. – С. 392-399.

8. Философский энциклопедический словарь. – М., 1989. – С. 460-461.

На опыте получены значения x и y, сведенные в таблицу

x
y	5,2	6,3	7,1	8,5	9,2	10,0

Найти прямую (2) по методу наименьших квадратов.

Решение. Находим:

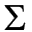x_i=21, 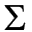y_i=46,3, 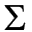x_i²=91, 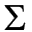x_iy_i=179,1.

Записываем уравнения (8) и (9)

91a+21b=179,1,

21a+6b=46,3,

отсюда находим

a=0,98 b=4,3.

Дадим оценку точности метода для линейного случая, когда имеет место уравнение (2).

Пусть опытные значения x_i являются точными, а опытные значения y_i имеют случайные ошибки с одинаковой дисперсией 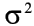для всех i.

Введем обозначение

(16)

Тогда решения уравнений (8) и (9) можно представить в виде

	(17)
	(18)
где
	(19)
Из уравнения (17) находим
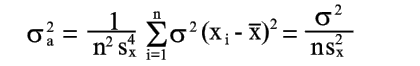
	(20)
Аналогично из уравнения (18) получаем
	(21)
так как
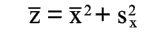
	(22)
Из уравнений (21) и (22) находим
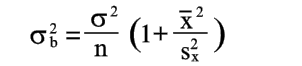
	(23)

Уравнения (20) и (23) дают оценку точности коэффициентов, определенных по уравнениям (8) и (9).

Заметим, что коэффициенты a и b коррелированы. Путем простых преобразований находим их корреляционный момент.

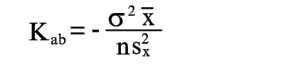
(24)

Уравнения (20), (23) и (24) позволяют найти оценку для ошибки y, которую дает уравнение (2) в произвольной точке x, если коэффициенты a и b найдены по уравнениям (8) и (9). Из уравнений (2), (20), (23) и (24) находим

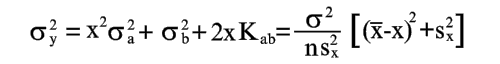
(25)

На основании уравнений (20), (23) и (25) можно сделать следующие выводы:

1.Точность коэффициентов a и b тем выше, чем больше s_x, т.е. чем больше рассеивание опытных точек на оси x.

2.Точность коэффициента b тем выше, чем меньше .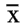

3.Ошибка уравнения (2) наименьшая в точке, где 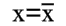, и наибольшая в точках, где величина 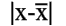имеет наибольшее значение.

Рассмотрим на примере использование уравнений (20)-(25).

Дата добавления: 2013-12-13