Макроскопические модели дорожного движения

Модели динамики транспортного потока

ЛЕКЦИЯ 3

Большинство существующих моделей динамики транспортных потоков может быть приблизительно разделено на три класса:

- макроскопические (гидродинамические) модели

- кинетические (газодинамические) модели

- микроскопические модели

Макроскопическими называют модели, которые описывают движение автомобилей в усредненных терминах, таких как плотность, средняя скорость, поток и др. При таком подходе транспортный поток уподобляется движению специфической жидкости, поэтому модели этого класса также называют гидродинамическими.

Микроскопическими называются модели, в которых явно моделируется движение каждого автомобиля. Такой подход позволяет теоретически достичь более точного описания движения автомобилей по сравнению с усредненным макроописанием, однако этот подход требует больших вычислительных ресурсов при практических применениях.

Промежуточное место занимает кинетический подход, при котором поток описывается плотностью распределения автомобилей в фазовом пространстве, т.е. пространстве координат и скоростей автомобилей. Динамика фазовой плотности описывается кинетическим уравнением. Это уравнение основано на усредненном описании эффектов взаимодействий индивидуальных автомобилей, и в этом смысле оно ближе к микроуровню, чем гидродинамические уравнения. Важное теоретическое значение кинетических моделей состоит в том, что на их основе можно систематически выводить макроскопические модели.

Особое место в классе микромоделей занимают модели типа клеточных автоматов (Cellural Automata), получившие широкое развитие в последние годы. В этих моделях принято чрезвычайно упрощенное дискретное во времени и пространстве описание движения автомобилей, за счет чего достигается высокая вычислительная эффективность.

Первая макроскопическая модель, основанная на гидродинамической аналогии, была предложена в 1955 в. Модель известна в научной литературе как LW-модель, названная так по именам авторов (Lighthill и Whitham). Обозначим через ρ(x; t) — плотность, V (x; t) — среднюю скорость автомобилей в точке дороги с координатой x в момент времени t. Эти величины связаны уравнением непрерывности, выражающим «закон сохранения количества автомобилей» на дороге:

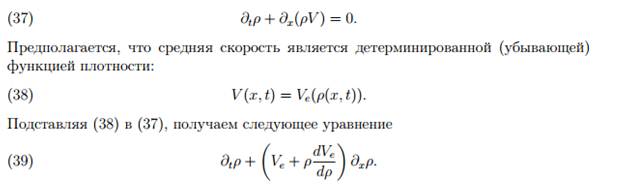
Уравнение (39) описывает распространение нелинейных кинематических волн со скоростью переноса c(ρ) = Ve(ρ) + ρdVe=dρ. С течением времени профиль волны может становиться все более крутым, вплоть до вертикального угла наклона, при котором образуется разрывный профиль волны (шоковые волны). Во многих работах разные варианты модели с шоковыми волнами были использованы для описания динамики заторов. Хотя первоначальная LW-модель представляется в настоящее время черезчур упрощенной, именно простота реализации делает возможным использование этой модели как вспомогательного инструмента при моделировании динамики загрузки больших транспортных сетей.

В реальности плотность автомобилей как правило не меняется скачками, а является непрерывной функцией координат и времени. Для устранения шоковых волн в уравнение (39) был добавлен член второго порядка, описывающий диффузию плотности, который приводит к сглаживанию профиля волны:

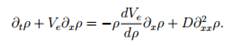(40)

Наиболее важным недостатком модели является соотношение (38), которое предполагает, что средняя скорость потока V (x; t) в каждый момент времени соответствует равновесному значению Ve при данной плотности автомобилей. Поэтому данная модель не адекватна реальности при описании неравновесных ситуаций, возникающих вблизи неоднородностей дороги (съезды и выезды, сужения), а также в условиях так называемого «stop-and-go» движения.

Для описания неравновесных ситуаций вместо детерминированного соотношения (38) было предложено использовать дифференциальное уравнение для моделирования динамики средней скорости. Впервые предложенное в 1971 в уравнение скорости имело вид:

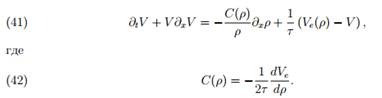
Данное уравнение было выведено на основе микроскопического описания движения отдельных автомобилей в соответствии с моделью «следование за лидером». Слагаемое V δ_xV называется конвекционным и описывает изменение скорости в данном месте дороги за счет кинематического переноса автомобилей из предшествующего сегмента дороги в данную точку со средней скоростью потока. Первое слагаемое в правой части называется «упреждающим» (anticipation); оно описывает реакцию водителей (торможение или ускорение) на изменение ситуации впереди.

Второе слагаемое в правой части называется релаксационным и описывает тенденцию приближения средней скорости V к равновесному при данной плотности значению Ve(ρ); ρ - характерное время релаксации.

Впоследствии было предложено значительное количество различных модификаций уравнения скорости, а также численного метода для его решения. Одним из наиболее существенных недостатков уравнения Пэйна является то, что стационарное однородное решение ρ(x; t) ≡ρ₀; V (x; t) ≡ Ve(ρ₀) является устойчивым в линейном приближении к малым возмущениям при всех значениях плотности. Однако анализ эмпирических данных показывает, что при высоких значениях плотности ламинарное движение транспортного потока становится неустойчивым, и малые возмущения приводят к возникновению фантомных заторов, или волн stopand-go движения. Данная проблема может быть преодолена следующим изменением в «упреждающем» члене уравнения:

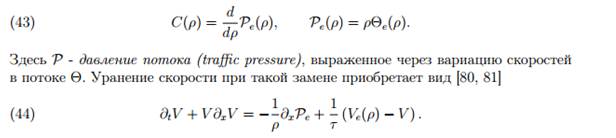
Согласно этому уравнению автомобили замедляют свое движение, если давление потока впереди возрастает, и ускоряют в противном случае. Предполагается, что вариация скоростей Ө зависит от плотности потока. Для этой зависимости применяются различные приближения, полученные из анализа эмпирических данных. В частности, в моделях в качестве первого приближения используется положительная константа: Ө_e(Ө) = Ө ₀.

Уравнение (44), так же как и (37)-(38), предсказывает возникновение шоковых волн. Для сглаживания и предотвращения разрывов решений в правую часть уравнения добавляется диффузионное слагаемое вида vδ²_xxV, аналогичное слагаемому, описывающему вязкость в уравнениях классической гидродинамики. Окончательно уравнение скоростей приобретает вид:

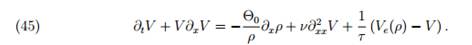(45)

Анализ устойчивости стационарного однородного решения данного уравнения показывает, что при значениях плотности, превышающих некоторое критическое значение ρcr, решение становится неустойчивым к малым возмущениям (область неустойчивости и инкремент возрастания зависят также от длины волны возмущения). Это обстоятельство позволяет теоретически моделировать эффекты, связанные с фантомными заторами, возникающими в однородном потоке в результате случайных возмущений.

Наиболее известной в рассматриваемом классе моделей является KK-модель

(модель Kerner-Konh¨auser,). Формулировка модели заключается в уравнениях (37),(45), в которых для большей совместимости с уравнением Навье-Стокса классической гидродинамики вместо константы ρ используется выражение ρ(ρ) = ρ₀=ρ, где ρ₀ - коэффициент вязкости.

Анализ устойчивости стационарного однородного решения KK-модели показывает устойчивость этого решения при малых и очень больших значениях плотности, а также наличие области неустойчивости при средних значениях плотности. На основе компьютерных расчетов с использованием данной модели изучен процесс образования и развития кластеров — изолированных перемещающихся областей с высокой плотностью и низкой скоростью потока.

Все рассмотренные модели не свободны, однако, от некоторых качественных недостатков. Например, при некоторых значениях параметров эти модели могут предсказывать плотности, превышающие максимально допустимые («бампер к бамперу»).

Кроме того, при сильных пространственных неоднородностях начальных условий могут возникать отрицательные значения скоростей (затор «рассасывается назад» как результат действия вязкости).

Описанные выше макроскопические модели сформулированы в основном на основе аналогий с уравнениями классической гидродинамики. Существует еще способ вывода макроскопических моделей из описания процесса взаимодействия автомобилей на микроуровне с использованием кинетического уравнения. Этот подход был предложен Пригожиным по аналогии с выводом в статистической физике уравнений динамики газа из кинетического уравнения для фазовой плотности. Таким путем могут быть получены некоторые из перечисленных выше моделей, а также модели существенно более детальные, например, включающие дифференциальные уравнения для описания динамики вариации скоростей, а также модели многополосного движения и др.

Дата добавления: 2013-12-13