Десятичная запись приближенных значений

Форма записи А = а ± D _а приближенного значения числа не всегда удобна. Целесообразно установить такой способ записи, который позволил бы по десятичной записи числа определить абсолютную погрешность приближения.

Введем понятие о верных цифрах приближенного значения числа.

Цифра α в десятичной записи приближенного значения величины х называется верной в широком смысле, если абсолютная погрешность приближения не превосходит единицы того разряда, которому принадлежит α.

Пример. Пусть х= 7,158±0, 0009. Так как Δ _а =0,0009<0,001, то все цифры числа а=7,158 – приближенного значения числа х верны в широком смысле.

Цифра α в десятичной записи приближенного значения величины х называется верной в строгом смысле, если абсолютная погрешность приближения не превосходит половины единицы того разряда, которому принадлежит α.

Пример. Пусть а= 3,142 – приближенное значение числа π = 3,14159 … Погрешность приближения Δ<0,000141<0,0005 = ½ ∙0,001, поэтому все цифры приближенного значения числа π верны в строгом смысле.

Цифры в записи приближенного значения числа, о которых нам неизвестно, являются ли они верными или нет, называются сомнительными.

Термин "верная цифра" не следует понимать буквально: верная цифра может и не совпадать с цифрой соответствующего разряда точного значения числа.

Пусть а = 3,1416 – приближенное значение числа
π = 3,14159….

Все цифры числа 3,1416 верные, хотя цифра десятитысячных (цифра 6) приближенного значения числа не совпадает с цифрой десятитысячных (цифрой 5)записи точного значения числа.

Правило: при десятичной записи приближенного значения числа записывают только верные цифры.

При наличии одной верной цифры допустимо принимать относительную ошибку числа близкой к 10%, двух – около 1%, трех – около 0,1% и т.д.

Значащими цифрами числа, записанного в виде десятичной дроби, называют все его верные цифры, начиная с первой слева, отличной от нуля.

Пример. Числа 3,78; 0,000207; 564; 0,300 по три значащие цифры, если все эти цифры верные.

Замечание. На практике предельная абсолютная или относительная погрешности задаются конкретным числом до начала вычисления (измерения). Процесс вычисления (измерения) продолжается до тех пор, пока не будут достигнуты условия (3), (8).

При операциях с приближенными числами ошибки результатов зависят от ошибок самих чисел.

Ошибки суммы.

1). Абсолютная ошибка суммы равна сумме абсолютных ошибок слагаемых:

D_с = D₁ + D₂ +…+ D_n

Для примера рассмотрим сумму двух приближенных значений:

А₁=а₁±D₁,

А₂= а₂±D₂, тогда

а₁-D₁ ≤ А₁ ≤ а₁+D₁

а₂-D₂ ≤ А₂ ≤ а₂+D₂

(а₁+а₂)-(D₁+D₂) ≤ А₁+А₂≤(а₁+а₂)+(D₁+D₂),

т.е. А₁+А₂ = (а₁+а₂)±(D₁+D₂),

значит для суммы п слагаемых: D_с = D₁ + D₂ +…+ D_n

2). Относительная ошибка суммы равна

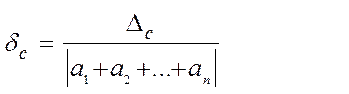
и заключена между минимальной и максимальной относительными ошибками слагаемых.

Дата добавления: 2013-12-13