Решение. 1. Выделяем все логические союзы:

1. Выделяем все логические союзы:

Если мне повезет и в моей руке будет туз, то в твоей будет джокер.

2. Вводим символическое обозначение для простых высказываний (суждений):

· "мне повезет" – а;

· "в моей руке будет туз" – b;

· "в твоей будет джокер" – с.

3. Делаем символическую запись: a & b ® c.

Таблицы истинности. Истинность сложных суждений зависит от истинности входящих в его состав простых суждений. В следующих таблицах показана истинность для каждого типа суждения.

a	b	a & b
Л	Л	Л
Л	И	Л
И	Л	Л
И	И	И
Рис.3.3. Конъюнкция

В конъюнктивных высказываниях вида " а&b " утверждается одновременное наличие двух положений дел – описываемого в а и в b. Таким образом, если два положения дел имеют место в действительности (то есть а и b истинны), то конъюнктивное высказывание " а & b " является истинным. Если же, по крайней мере, одно положение дел отсутствует (то есть или а, или b, или а и b одновременно ложны), то и общее конъюнктивное высказывание – ложно. Формулировка конъюнктивных высказываний в русском языке обычно осуществляется с помощью союза " И ". Например, высказывание "“2 ” – простое число и “ 2 ” – четное число" истинно, поскольку обе его части – истинные высказывания. А ложным высказыванием будет такое "“3 ” – простое число и “3” – четное число", поскольку в данном случае второе высказывание ложно.

a	b	a V b
Л	Л	Л
Л	И	И
И	Л	И
И	И	И
Рис.3.4. Дизъюнкция

Логическое дизъюнктивное высказывание " а V b " выражает мысль о наличии по крайней мере одного из двух положений дел – описываемого в a или описываемого в b. При этом не исключается случай их одновременного наличия. Высказывание " а V b " истинно, если истинно хотя бы одно из высказываний – а или b. В том же случае, когда оба высказывания дизъюнкции ложны, то и сложное высказывание ложно. Данному логическому союзу в русском языке обычно соответствует союз " ИЛИ ". Например, высказывание "Я получу на экзаменах “ 4 ” ИЛИ “ 5 ” " будет истинным, если выполняется хотя бы одно из выражений.

В некоторых контекстах естественного языка союз " ИЛИ " имеет иной смысл. Так, в высказывании "Храбрец иль сидит в седле, иль тихо спит в сырой земле" выражается мысль о наличии только одной из двух ситуаций, то есть утверждается их альтернативность, невозможность одновременного осуществления положения этих дел. В этих случаях союз "ИЛИ" не может быть заменен дизъюнкцией, ему будет соответствовать иной логический союз, который называется строгой дизъюнкцией.

a	b	a V b
Л	Л	Л
Л	И	И
И	Л	И
И	И	Л
Рис.3.5. Строгая дизъюнкция

Логическое строго дизъюнктивное высказывание вида ″ а V b ″ выражает утверждение о наличии только одной из двух ситуаций, описанной в а или описанной в b. Данное выражение является истинным в следующих двух случаях:
1) когда а – истинно, а b – ложно или 2) когда b -истинно, а а – ложно, то есть когда а и b имеют различные значения. Если же значения двух высказываний а и b совпадают, то есть они одновременно истинны или одновременно ложны, то значение выражения (а V b) принимает значение "ложь".

a	b	a ® b
Л	Л	И
Л	И	Л
И	Л	И
И	И	И
Рис.3.6. Импликация

Для обозначения сложных высказываний, в которых утверждается, что наличие одной ситуации обуславливает наличие другой, вводится импликативное высказывание вида (а®b). Данное логическое выражение эквивалентным образом можно переформулировать так: не имеет места ситуация, при которой положение дел, описываемое в а, существует, а положение дел, описываемое в b, отсутствует. Отсюда следует, что при истинном а и ложном b высказывание (а → b) ложно. В естественном языке, наиболее адекватно отражающим смысл импликации, является союз " ЕСЛИ..., ТО ". В выражениях (а → b) высказывание а называется основанием (или антецедентом), а b – следствием (или консеквентном). В предложениях основание не всегда предшествует следствию, например, в высказывании "Вылет будет задержан, если не улучшится погода" следствием является первая часть высказывания, а основанием – вторая.

a	b	а º b
Л	Л	И
Л	И	Л
И	Л	Л
И	И	И
Рис.3.7. Эквиваленция

И наконец, для обозначения отношений равнозначности высказываний используются эквивалентные высказывания вида " а º b ". Данное сложное высказывание будет истинным в том случае, если будут одновременно истинными или одновременно ложными оба высказывания. Формула " а º b " означает, что истинность высказывания а достаточна для признания истинности высказывания b, и наоборот. А также, что ложность высказывания а достаточна для признания ложности высказывания b. Например, эквивалентным высказыванием будет следующее высказывание "если и только еслисумма цифр числа делится на три, то и само число делится на три". В данном выражении эквиваленция задается союзом " ЕСЛИ И ТОЛЬКО ЕСЛИ…, ТО ", но возможно также выражение эквиваленции и с помощью следующего выражения русского языка – " ДЛЯ ТОГО ЧТОБЫ … НЕОБХОДИМО И ДОСТАТОЧНО, ЧТОБЫ … ". Последнее часто используется в математике и естествознании при формулировке законов.

a	ā
И	Л
Л	И
Рис.3.8. Инверсия

Отрицание исходного суждения осуществляется путем логической инверсии, сущность которой заключается в введении или удалении инверсной связки. Суждение является отрицательным, если оно не может быть истинным и ложным одновременно с исходным суждением. Например, высказывание "Я не говорил правду" является отрицанием высказывания "Я говорил правду", поскольку при истинности одного из этих высказываний другое обязательно ложно. А в следующем примере высказывание "Некоторые люди не говорят правду" не является отрицанием высказывания "Все люди говорят правду", так как данная пара суждений может быть одновременно ложной.

Отрицание простых и сложных суждений. Отрицание суждений – это логическая операция, заключающаяся в преобразовании логического содержания суждения, в результате которого истинное суждение становится ложным, а ложное – истинным. Другими словами, меняется истинностное значение суждения. В этом случае исходное суждение называется отрицаемым, а результирующее - отрицающим.

Легче всего ввести отрицание для экзистенциального суждения – достаточно преобразовать суждение, утверждающее факт существования, в суждение его отрицающее, и наоборот. Например, если дан тезис "Мамонты существуют", то его отрицанием будет "Мамонты не существуют".

Отрицание простых общих и частных атрибутивных суждений осуществляется по следующим схемам, построенным на основе логического квадрата:

_ _ _ _ A → O; E→ I; I → O; O → I.

Например, общее суждение "Неверно, что все люди братья" будет преобразовано путем отрицания в отрицающее суждение "Некоторые люди не являются братьями". По несколько иным схемам осуществляется отрицание простых единичных суждений. В этих суждениях происходит замена внешней инверсии на внутреннюю, при этом двойное отрицание опускается. Например, суждение "Неверно, что Курск не является областным центром" в результате отрицания будет преобразовано в суждение "Курск является областным центром".

В том случае, когда суждение является реляционным, отрицание будет представлено как суждение с отрицанием наличия отношения (например, тезис "Иван брат Петра" преобразуется в антитезис "Иван не брат Петра") или же как суждение с заменой отношений на противоположные (например, тезис "Число X больше числа Y" преобразуется в антитезис "Число X меньше или равно числу Y").

Отрицание сложных конъюнктивных и дизъюнктивных суждений осуществляется по так называемым правилам де Моргана. Результатом отрицания конъюнктивного суждения является дизъюнктивное суждение, в котором составляющие суждения являются отрицанием составляющих исходного конъюнктивного суждения (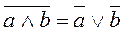). Результатом отрицания дизъюнктивного суждения является конъюнктивное суждение, в котором составляющие суждения являются отрицанием составляющих исходного дизъюнктивного суждения (). При отрицании строго дизъюнктивного суждения получается эквивалентное суждение (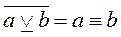). Наоборот, отрицание эквивалентного суждения дает строго дизъюнктивное (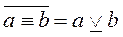). Результатом отрицания импликативного суждения является конъюнктивное суждение, в котором одним из составляющих суждений является "причина" исходного суждения, а вторым – отрицание "следствия" исходного суждения ().

Логическая операция отрицания замены широко используется в научной практике. Так, в юриспруденции часто вместо доказательства виновности подозреваемого в совершении преступления прибегают к доказательству его невиновности.

Задание 6. Введите отрицание следующего суждения:

Все студенты изучают логику и математику.

Дата добавления: 2013-12-13