
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства меры Жордана
|
|
|
|
Площадь фигуры (плоская мера Жордана).
Фиксируем на плоскости прямоугольную декартову систему координат  . Разобьём плоскость на квадраты прямыми линиями
. Разобьём плоскость на квадраты прямыми линиями  . Назовём их квадратами ранга 0. Площадь каждого квадрата равна
. Назовём их квадратами ранга 0. Площадь каждого квадрата равна  .
.
Разбивая стороны квадратов ранга 0 на 10 равных частей, получим разбиение плоскости на квадраты ранга 1, площади 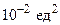 и т.д. Площадь каждого квадрата ранга
и т.д. Площадь каждого квадрата ранга  равна
равна  .
.
Пусть  − ограниченное множество на плоскости. Обозначим
− ограниченное множество на плоскости. Обозначим  , где
, где  − число квадратов ранга
− число квадратов ранга  , принадлежащих множеству
, принадлежащих множеству  . Обозначим
. Обозначим  , где
, где 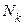 − число квадратов ранга
− число квадратов ранга  , пересекающихся с множеством
, пересекающихся с множеством  .
.

Ясно, что 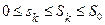 .
.
Определение 1. Величина  называется внутренней меройЖордана множества
называется внутренней меройЖордана множества  . Величина
. Величина 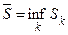 называется внешней меройЖордана множества
называется внешней меройЖордана множества  .
.
Определение 2. Множество  измеримо по Жордану, если
измеримо по Жордану, если 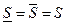 . В этом случае число
. В этом случае число  называется просто меройЖордана или площадью множества
называется просто меройЖордана или площадью множества  .
.
- Неотрицательность
 .
. - Аддитивность
 .
. - Монотонность
 (а также
(а также  и
и  ) по включению.
) по включению. - Инвариантность
 относительно сдвигов, поворотов и симметрий.
относительно сдвигов, поворотов и симметрий.
Следствие. Мера  не зависит от выбора ортонормированного базиса
не зависит от выбора ортонормированного базиса  .
.
Упражнение. Прямоугольник  − измеримое множество, при этом
− измеримое множество, при этом  .
.
Теорема. Пусть  и пусть
и пусть  . В таком случае криволинейная трапеция
. В таком случае криволинейная трапеция  − измеримое множество и площадь этого множества равна
− измеримое множество и площадь этого множества равна 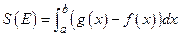 .
.
Доказательство. В доказываемой формуле ничего не изменится, если добавить к обеим функциям произвольную константу. Поэтому при доказательстве можно считать, что  . Далее, ввиду аддитивности меры Жордана достаточно найти площадь фигуры
. Далее, ввиду аддитивности меры Жордана достаточно найти площадь фигуры  .
.
Рассмотрим разбиение 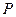 отрезка
отрезка  и связанные с ним ступенчатые фигуры
и связанные с ним ступенчатые фигуры  , отличающиеся тем, что на
, отличающиеся тем, что на  частичном промежутке
частичном промежутке 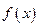 в первом случае заменяется
в первом случае заменяется 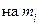 , во втором −
, во втором − 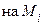 . Ввиду свойства монотонности имеем
. Ввиду свойства монотонности имеем
 .
.
С другой стороны,  . Критерий интегрируемости показывает, что
. Критерий интегрируемости показывает, что  и что
и что 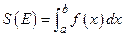 . Ч. и т.д.
. Ч. и т.д.

Определение. Область на плоскости называется простой в заданном направлении, если её пересечение с каждой прямой данного направления представляет собой отрезок, точку либо пустое множество.
Теорема 2. Пусть  − область плоскости
− область плоскости 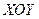 , простая по обоим координатным направлениям, граница которой − гладкая замкнутая кривая
, простая по обоим координатным направлениям, граница которой − гладкая замкнутая кривая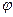 , заданная параметрическими уравнениями:
, заданная параметрическими уравнениями:
 .
.
Если при увеличении  точка
точка  обходит границу области против движения часовой стрелки, то площадь области равна
обходит границу области против движения часовой стрелки, то площадь области равна

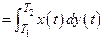
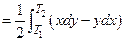 .
.
Доказательство. Продолжим  периодически с периодом
периодически с периодом  . Можно считать, что
. Можно считать, что  − крайние значения функции
− крайние значения функции  . Теперь первая из формул следует из теоремы 1 с помощью замены переменной интегрирования. Нужно только воспользоваться свойством аддитивности меры. Вторая формула выводится точно так же, а третья − следует из первых двух.
. Теперь первая из формул следует из теоремы 1 с помощью замены переменной интегрирования. Нужно только воспользоваться свойством аддитивности меры. Вторая формула выводится точно так же, а третья − следует из первых двух.
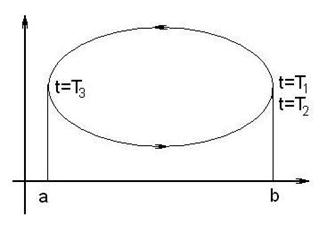
Теорема 3. Если фигура  ограниченна лучами
ограниченна лучами  ,
,  и кривой с уравнением в полярных координатах
и кривой с уравнением в полярных координатах 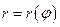 , где
, где  , то её площадь равна
, то её площадь равна
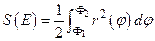 .
.

Доказательство. Рассмотрим разбиение 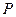 отрезка
отрезка  и заменим множество
и заменим множество  фигурами
фигурами 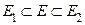 , состоящими не из прямоугольников, как в теореме 1, а из круговых секторов
, состоящими не из прямоугольников, как в теореме 1, а из круговых секторов  и
и  . Так как площадь сектора радиуса
. Так как площадь сектора радиуса  с центральным углом
с центральным углом 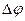 равна
равна  , то, рассуждая, как при доказательстве теоремы 1, получим
, то, рассуждая, как при доказательстве теоремы 1, получим 

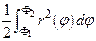 .
.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 2357; Нарушение авторских прав?; Мы поможем в написании вашей работы!