Коэффициент корреляции. Коэффициент корреляции рангов, предложенный к Спирменом, относится к непараметрическим показателям связи между переменными

КОРРЕЛЯЦИИ СПИРМЕНА

РАНГОВЫЙ КОЭФФИЦИЕНТ

Коэффициент корреляции рангов, предложенный К Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин Правила ранжирования варьирующих величин были описаны выше.

Величина коэффициента линейной корреляции Спирмена также лежит в интервале +1 и -1 Он, как и коэффициент Пирсона, может быть положительным и отрицательным, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале

В принципе число ранжируемых признаков (качеств, черт и т п) может быть любым, но сам процесс ранжирования большего чем 20 числа признаков — затруднителен Возможно, что именно поэтому таблица критических значений рангового коэффициента корреляции рассчитана лишь для сорока ранжируемых признаков (n < 40). В случае использования большего, чем 40 числа ранжируемых признаков, уровень значимости коэффициента корреляции следует находить с использованием пакетов прикладных программ.

Ранговый коэффициент линейной корреляции Спирмена подсчитывается по формуле:

.

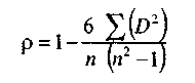где n — количество ранжируемых признаков (показателей, испытуемых)

D — разность между рангами по двум переменным для каждого испытуемого

Σ(D²) — сумма квадратов разностей рангов.

«τ» (тау) КЕНДАЛЛА

Коэффициент корреляции «τ» (тау) Кендалла относится к числу непараметрических, т е при вычислении этого коэффициента не играет роли характер распределения сравниваемых переменных Коэффициент τ предназначен для работы с данными, полученными в ранговой шкале Иногда этот коэффициент можно использовать вместо коэффициента корреляции Спирмена, поскольку способ его вычисления более прост он основан на вычислении суммы инверсий и совпадений.

Таблица возможного использования коэффициентов корреляции приведена ниже.

Тип шкалы	Какой коэффициент использовать
Переменная X	Переменная Y
Интервальная или отношений	Интервальная или отношений	Коэффициент Пирсона r x y
Ранговая, интервальная или отношений	Ранговая, интервальная или отношений	Коэффициент Спирмена ρ x y
Ранговая	Ранговая	Коэффициент «τ» Кендалла

Дата добавления: 2013-12-13