
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 18. Последовательности. Пределы последовательностей и их свойства
|
|
|
|
Пусть x – переменная величина. Это значит, что величина x меняет свои значения. Этим она принципиально отличается от любой постоянной величины a, которая своего неизменного значения не меняет. Например, высота столба – величина постоянная, а высота живого растущего дерева – величина переменная.
Переменная величина x считается заданной, задана числовая последовательность
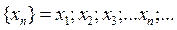 (1)
(1)
ее значений. То есть тех значений x 1; x 2; x 3;…, которые она последовательно, одно за другим, принимает в процессе своего изменения. Будем считать, что этот процесс изменения величиной x своих значений ни на каком этапе не прекращается (переменная х никогда не застывает, она «всегда живая»). А это значит, что последовательность (1) имеет бесконечное число значений, что и отмечено в (1) многоточием.
Значения переменной величины можно рассматривать как множество значений функции натурального аргумента xn=f(n). Член xn называется общим членом последовательности. Последовательность считается заданной, если дан способ вычисления любого её члена по его известному номеру.
Пример 1: Написать первые десять членов последовательности, если её общий член .
.
Решение: Вычисляя значение дроби  при значениях n равных 1,2,3,…10, получим:
при значениях n равных 1,2,3,…10, получим:

Вообще же последовательность с общим членом  запишется так:
запишется так: 
Естественно, возникает интерес относительно характера изменения величиной x своих значений. То есть возникает вопрос: меняются эти значения бессистемно, хаотически или все же как-то целенаправленно.
Основной интерес представляет, конечно, второй вариант. А именно, пусть значения xn переменной x по мере увеличения их номера n неограниченно приближаются (стремятся) к некоторому конкретному числу a. Это значит, что разность (расстояние) между значениями xn переменной x и числом a сокращается, стремясь при увеличении n (при 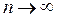 ) к нулю. Заменяя слово «стремится» стрелкой, сказанное выше можно записать так:
) к нулю. Заменяя слово «стремится» стрелкой, сказанное выше можно записать так:
 при
при 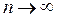 <=>
<=> 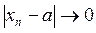 при
при 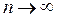 (2)
(2)
Если имеет место (2), то говорят, что переменная х стремится к числу а. Это число а называется пределом переменной x. И записывается это следующим образом:
 <=>
<=>  (3)
(3)
Читается: предел x равен a (x стремится к a).
Стремление переменной x к своему пределу a можно наглядно проиллюстрировать на числовой оси. 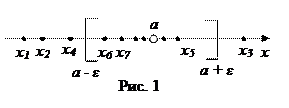 Точный математический смысл этого стремления x к a состоит в том, что какое бы малое положительное число
Точный математический смысл этого стремления x к a состоит в том, что какое бы малое положительное число 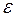 ни взять, а значит, каким бы малым промежутком
ни взять, а значит, каким бы малым промежутком  ни окружить на числовой оси число a, в этот промежуток (в так называемую
ни окружить на числовой оси число a, в этот промежуток (в так называемую 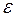 -окрестность числа a) попадут, начиная с некоторого номера N, все значения xn переменной x. В частности, на рис. 1 в изображенную
-окрестность числа a) попадут, начиная с некоторого номера N, все значения xn переменной x. В частности, на рис. 1 в изображенную 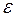 -окрестность числа a попали все значения xn переменной x, начиная с номера
-окрестность числа a попали все значения xn переменной x, начиная с номера  .
.
Определение: Число а называется пределом последовательности 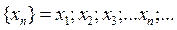 (пределом переменной х или пределом функции f(n)), если каково бы ни было наперед заданное положительное число
(пределом переменной х или пределом функции f(n)), если каково бы ни было наперед заданное положительное число  , всегда можно найти такое натуральное число N, что для всех членов последовательности с номерами n>N будет выполняться неравенство
, всегда можно найти такое натуральное число N, что для всех членов последовательности с номерами n>N будет выполняться неравенство  .
.
Это неравенство равносильно таким двум неравенствам:  . Число N зависит от выбранного
. Число N зависит от выбранного  . Если уменьшить число
. Если уменьшить число  , то соответствующий ему номер N увеличится.
, то соответствующий ему номер N увеличится.
Для последовательности (или для переменной х) необязательно иметь предел, но если этот предел есть, то он единственный. Имеющую предел последовательность называют сходящейся. Последовательность, не имеющую предела называют расходящейся.
Переменная величина x, может стремиться к своему пределу различными способами:
1. оставаясь меньше своего предела,
2. оставаясь больше своего предела,
3. колеблясь около своего предела,
4. принимая значения, равные своему пределу.
Выбор числа  произволен, но после того как оно выбрано, никаким изменениям в дальнейшем оно не должно подвергаться.
произволен, но после того как оно выбрано, никаким изменениям в дальнейшем оно не должно подвергаться.
Переменная x, имеющая своим пределом нуль (то есть стремящаяся к нулю) называется бесконечно малой. А переменная x, неограниченно растущая по абсолютной величине, называется бесконечно большой (ее модуль стремится к бесконечности).
Итак, если  , то x – бесконечно малая переменная величина, а если
, то x – бесконечно малая переменная величина, а если  , то x – бесконечно большая переменная величина. В частности, если
, то x – бесконечно большая переменная величина. В частности, если  или
или 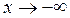 , то x – бесконечно большая переменная величина.
, то x – бесконечно большая переменная величина.
Если  , то
, то 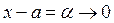 . И обратно, если
. И обратно, если 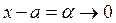 , то
, то  . Отсюда получаем следующую важную связь между переменной x и ее пределом a:
. Отсюда получаем следующую важную связь между переменной x и ее пределом a:
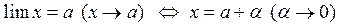 (4)
(4)
Уже говорилось, что не всякая переменная x имеет предел. У многих переменных нет предела. Есть он или нет – это зависит от того, какова последовательность (1) значений этой переменной.
Пример 2. Пусть
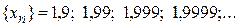
Здесь, очевидно, 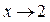 , то есть
, то есть 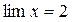 .
.
Пример 3. Пусть

Здесь, очевидно, 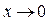 , то есть
, то есть  . Значит, переменная x – бесконечно малая.
. Значит, переменная x – бесконечно малая.
Пример 4. Пусть

Здесь, очевидно, 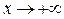 , то есть
, то есть 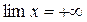 . Значит, переменная x – бесконечно большая.
. Значит, переменная x – бесконечно большая.
Пример 5. Пусть

Здесь, очевидно, переменная x ни к чему не стремится. То есть предела у нее нет (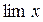 не существует).
не существует).
Пример 6. Пусть
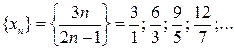
Здесь ситуация с пределом переменной x не так очевидна, как в предыдущих четырех примерах. Для прояснения этой ситуации преобразуем значения xn переменной x:

Очевидно, что 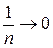 при
при 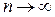 . Значит,
. Значит,
 при
при 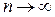 .
.
А это значит, что  , то есть
, то есть  .
.
Пример 7. Пусть
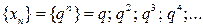
Здесь последовательность { xn } значений переменной x представляет собой бесконечную геометрическую прогрессию со знаменателем q. Следовательно, предел переменной x – это предел бесконечной геометрической прогрессии.
а) Если 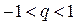 , то, очевидно,
, то, очевидно,  при
при 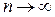 . А это значит, что
. А это значит, что 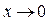 (
( ).
).
б) Если  , то
, то  . То есть в этом случае значения переменной x не меняются – они все время равны 1. Тогда и ее предел равен 1 (
. То есть в этом случае значения переменной x не меняются – они все время равны 1. Тогда и ее предел равен 1 ( ).
).
в) Если 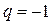 , то
, то  . В этом случае, очевидно,
. В этом случае, очевидно, 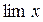 не существует.
не существует.
г) Если  , то
, то 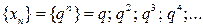 – бесконечно возрастающая положительная числовая последовательность. А значит,
– бесконечно возрастающая положительная числовая последовательность. А значит, 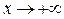 (
(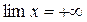 ).
).
д) Если 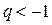 , то вводя обозначение
, то вводя обозначение  , где
, где 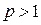 , получим:
, получим:  – знакопеременная числовая последовательность с бесконечно возрастающими по абсолютной величине членами:
– знакопеременная числовая последовательность с бесконечно возрастающими по абсолютной величине членами:
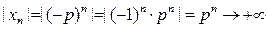 при
при 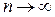
А значит, переменная x бесконечно большая. Но в силу знакопеременности ее членов она не стремится ни к +∞, ни к –∞ (предела не имеет).
Пример 8. Доказать, что последовательность с общим членом  имеет предел, равный 2.
имеет предел, равный 2.
Доказательство: Выберем произвольно положительное число  и покажем, что для него можно подобрать такое число N, что для всех значений номера n, больших этого числа N, будет выполняться неравенство
и покажем, что для него можно подобрать такое число N, что для всех значений номера n, больших этого числа N, будет выполняться неравенство  , в котором надо взять a=2,
, в котором надо взять a=2,  , т.е. будет выполняться неравенство
, т.е. будет выполняться неравенство 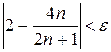 .
.
Из этого неравенства после приведения в скобках к общему знаменателю получаем 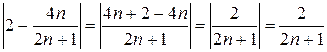 . Таким образом:
. Таким образом: 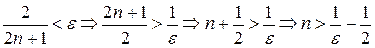 . За N возьмем наименьшее целое число принадлежащее интервалу
. За N возьмем наименьшее целое число принадлежащее интервалу  . Таким образом, мы сумели по произвольно заданному положительному
. Таким образом, мы сумели по произвольно заданному положительному  определить такое натуральное N, что неравенство
определить такое натуральное N, что неравенство 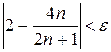 выполняется для всех номеров n>N. Этим и доказано, что 2 есть предел последовательности с общим членом
выполняется для всех номеров n>N. Этим и доказано, что 2 есть предел последовательности с общим членом  .
.
Отдельный интерес представляют монотонные и ограниченные последовательности.
Определение: последовательность называется монотонно возрастающей, если при всех n каждый её член больше предшествующего, т.е. если 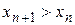 , и монотонно убывающей, если каждый ее член меньше предшествующего, т.е.
, и монотонно убывающей, если каждый ее член меньше предшествующего, т.е.  .
.
Пример 9. Последовательность натуральных чисел 1,2,3,…., n,… - монотонно возрастающая.
Пример 10. Последовательность чисел  , обратных натуральным,
, обратных натуральным, 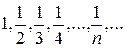 - монотонно убывающая.
- монотонно убывающая.
Определение: последовательность называется ограниченной, если все её члены находятся в конечном интервале (-М,+М) и М>0, т.е. если  , для любого номера n.
, для любого номера n.
Пример 11. Последовательность { xn }, где xn есть n -й десятичный знак числа  , ограничена, т.к.
, ограничена, т.к. 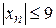 .
.
Пример 12. Последовательность 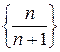 ограничена, так как
ограничена, так как 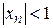 .
.
Основные свойства переменных величин и их пределов
1) Если  (переменная x неизменна и равна постоянной a), то естественно считать, что и
(переменная x неизменна и равна постоянной a), то естественно считать, что и  . То есть предел постоянной равен ей самой:
. То есть предел постоянной равен ей самой:
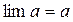 (5)
(5)
2) Если  ,
, 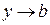 и a и b конечны, то
и a и b конечны, то 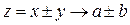 . То есть
. То есть
 (6)
(6)
(предел суммы или разности переменных равен сумме или разности их пределов).
3) Если  ,
, 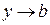 и a и b конечны, то
и a и b конечны, то 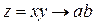 . То есть
. То есть
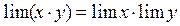 (7)
(7)
(предел произведения переменных равен произведению их пределов).
4) Если  ,
, 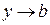 , a и b конечны и
, a и b конечны и  , то
, то  . То есть
. То есть
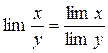 (8)
(8)
(предел частного равен частному пределов).
5) Если  ,
, 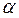 и
и  – любые постоянные числа, то
– любые постоянные числа, то 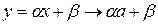 . То есть
. То есть
 (9)
(9)
Действительно, на основании предыдущих свойств имеем:
 .
.
6) Если x – бесконечно малая переменная величина (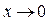 ), то
), то  – бесконечно большая переменная величина (
– бесконечно большая переменная величина ( ).
).
7) Если x – бесконечно большая переменная величина (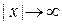 ), то
), то  – бесконечно малая переменная величина (
– бесконечно малая переменная величина ( ).
).
8) Если переменная x ограничена (это значит, что все ее значения xn расположены в некотором конечном числовом промежутке 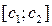 ), а переменная y бесконечно малая (
), а переменная y бесконечно малая ( ), то переменная
), то переменная  – тоже бесконечно малая (
– тоже бесконечно малая ( ).
).
9) Если переменная x ограничена, а переменная y бесконечно большая ( ), то переменная
), то переменная 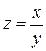 – бесконечно малая (
– бесконечно малая ( ).
).
10) Теорема Вейерштрасса.
а) Пусть значения xn переменной x монотонно возрастают и при этом все они меньше некоторой постоянной величины C. Такая переменная x называется монотонно возрастающей и ограниченной сверху (числом C). Она заведомо имеет конечный предел a, причем 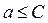 . Наглядную иллюстрацию этой ситуации дает рис. 2.
. Наглядную иллюстрацию этой ситуации дает рис. 2.
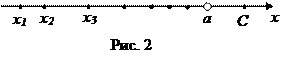
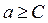 . Наглядную иллюстрацию этой ситуации дает рис. 3.
. Наглядную иллюстрацию этой ситуации дает рис. 3.

|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1103; Нарушение авторских прав?; Мы поможем в написании вашей работы!