
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Асимптоты графиков функций
|
|
|
|
Определение. Асимптоты графика функции – это такие линии (прямые или кривые), к которым неограниченно приближается указанный график при неограниченном его продолжении.
В частности, на рис. 8 изображен график функции  , имеющий три асимптоты: вертикальную прямую
, имеющий три асимптоты: вертикальную прямую 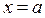 , горизонтальную прямую
, горизонтальную прямую  и кривую
и кривую 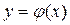 . При этом, согласно этого рисунка, вертикальная прямая
. При этом, согласно этого рисунка, вертикальная прямая 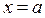 является асимптотой графика функции
является асимптотой графика функции  лишь при
лишь при  (при x, стремящемся к a справа). При
(при x, стремящемся к a справа). При 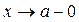 (слева) эта прямая асимптотой графика функции
(слева) эта прямая асимптотой графика функции  не является. Горизонтальная прямая
не является. Горизонтальная прямая  является асимптотой графика функции
является асимптотой графика функции  при
при  . А кривая
. А кривая 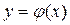 является асимптотой графика этой функции при
является асимптотой графика этой функции при  .
.

1. Нахождение вертикальных асимптот.
Рисунок 8 свидетельствует: если прямая 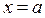 – вертикальная асимптота графика функции
– вертикальная асимптота графика функции  , то должны выполняться два условия:
, то должны выполняться два условия:
1) a – точка разрыва функции  ; (1)
; (1)
2) 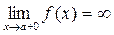 (+¥ или –¥) или
(+¥ или –¥) или 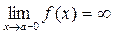 (+¥ или –¥).
(+¥ или –¥).
И обратно, если выполняются оба условия (1), то прямая 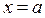 – вертикальная асимптота графика функции
– вертикальная асимптота графика функции  .
.
Из сказанного вытекает следующая схема нахождения вертикальных асимптот графика функции  :
:
1) Находим все точки разрыва (а 1; а 2; …) функции, то есть те изолированные точки оси ох, в которых функция не определена (ибо там, где элементарная функция определена, там она и непрерывна).
2) Каждую из точек разрыва проверяем на выполнимость второго условия (1).
Пример 5. Найти вертикальные асимптоты графика функции

и сделать геометрическую иллюстрацию полученного результата.
Решение. Данная функция не определена, а следовательно, разрывна лишь в двух точках оси ох:  и
и 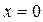 . Проверим каждую из них на выполнимость второго условия (1):
. Проверим каждую из них на выполнимость второго условия (1):
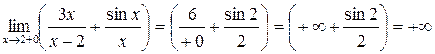

 ;
; 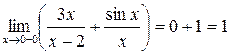 .
.
Второе условие (1) выполняется для точки  и не выполняется для точки
и не выполняется для точки 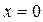 . Значит, лишь прямая
. Значит, лишь прямая  является вертикальной асимптотой графика нашей функции, причем и при
является вертикальной асимптотой графика нашей функции, причем и при  , и при
, и при 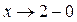 . А прямая
. А прямая 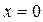 (ось оу) вертикальной асимптотой графика функции не является. Геометрическая иллюстрация полученных результатов дана на рис. 9.
(ось оу) вертикальной асимптотой графика функции не является. Геометрическая иллюстрация полученных результатов дана на рис. 9.
 На этом рисунке представлено лишь то, что выяснено выше: поведение функции y возле ее точек разрыва
На этом рисунке представлено лишь то, что выяснено выше: поведение функции y возле ее точек разрыва 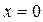 и
и  . Вдали от этих точек мы эту функцию не исследовали, поэтому ее график не известен (он лишь намечен пунктирной линией).
. Вдали от этих точек мы эту функцию не исследовали, поэтому ее график не известен (он лишь намечен пунктирной линией).
2. Нахождение наклонных (невертикальных) асимптот.
Рассматривая рис. 8, приходим к очевидному выводу: если некоторая линия L с уравнением 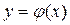 является невертикальной асимптотой графика функции
является невертикальной асимптотой графика функции  при
при  или при
или при  , то это значит, что при таком изменении x функция
, то это значит, что при таком изменении x функция  , то есть
, то есть  , а значит
, а значит
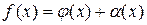 , где
, где 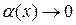 при
при  или при
или при  . (2)
. (2)
И обратно, при выполнении (2) функция 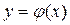 – асимптота функции
– асимптота функции  . В частности, если
. В частности, если
 , где
, где 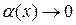 при
при  или при
или при  , (3)
, (3)
то соответственно при  или при
или при  горизонтальная прямая
горизонтальная прямая 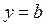 будет асимптотой графика функции
будет асимптотой графика функции  .
.
Пример 6. Найти невертикальные асимптоты графика функции
 .
.
Решение. Для их нахождения нужно выяснить поведение функции y при  и при
и при  .
.
а) Если  , то очевидно, что
, то очевидно, что
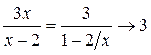 ;
; 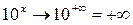 .
.
Поэтому при  функция
функция 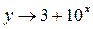 . А это значит, что линия L с уравнением
. А это значит, что линия L с уравнением  является асимптотой графика нашей функции при
является асимптотой графика нашей функции при  .
.
б) Если  , то очевидно, что
, то очевидно, что
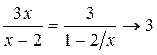 ;
; 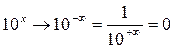 .
.
Поэтому при  наша функция
наша функция 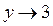 . А это значит, что при
. А это значит, что при  асимптотой графика нашей функции y является горизонтальная прямая
асимптотой графика нашей функции y является горизонтальная прямая  .
.
Пример 7. Определить все имеющиеся асимптоты графика функции 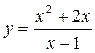 и изобразить поведение этого графика возле его асимптот.
и изобразить поведение этого графика возле его асимптот.
Решение. Начнем с нахождения области определения функции y. Функция определена, а следовательно, и непрерывна для всех x, кроме 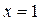 . То есть
. То есть 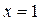 – единственная точка разрыва нашей функции. А значит, вертикальная прямая
– единственная точка разрыва нашей функции. А значит, вертикальная прямая 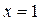 , проходящая через эту точку – единственная возможная вертикальная асимптота графика нашей функции.
, проходящая через эту точку – единственная возможная вертикальная асимптота графика нашей функции.
Проверим, действительно ли она – вертикальная асимптота. Для этого выясним, в соответствии с (1), поведение функции y при 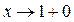 и при
и при 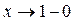 :
:
 ;
; 
То есть  при
при 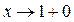 и
и  при
при 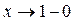 . А это значит, что вертикальная прямая
. А это значит, что вертикальная прямая 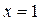 является асимптотой графика функции y, причем и при
является асимптотой графика функции y, причем и при 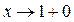 , и при
, и при 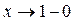 .
.
Теперь поищем возможные невертикальные асимптоты. Для этого рассмотрим поведение функции y при  и при
и при  .
.
а) Если  , то
, то
 .
.
Учтем, что 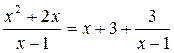 (это устанавливается делением
(это устанавливается делением 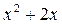 на
на  «в столбик»). То есть
«в столбик»). То есть
 , где
, где  ,
, 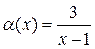 .
.
И так как 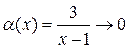 при
при  , а
, а 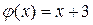 при
при  к нулю не стремится, то при
к нулю не стремится, то при  наша функция
наша функция 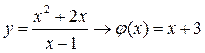 . А это, в соответствии с (2), означает, что линия с уравнением
. А это, в соответствии с (2), означает, что линия с уравнением  (прямая) является асимптотой графика нашей функции y при
(прямая) является асимптотой графика нашей функции y при  .
.
б) Если  , то буквально повторяя (а), приходим к выводу, что прямая
, то буквально повторяя (а), приходим к выводу, что прямая 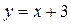 является асимптотой графика нашей функции и при
является асимптотой графика нашей функции и при  .
.
Теперь изобразим график нашей функции вместе с его асимптотами. Для более качественного построения этого графика найдем еще точки его пересечения с осями координат.
1) С осью ох:
 .
.
2) 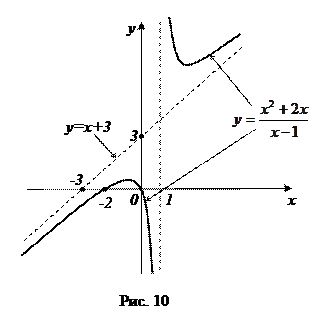 С осью оу:
С осью оу:
 .
.
А теперь строим график (рис. 10).
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 637; Нарушение авторских прав?; Мы поможем в написании вашей работы!