Упражнения. Найти асимптоты графиков функций

Найти асимптоты графиков функций

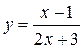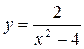а) ; б) ; в)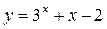

и построить эти графики вместе с их асимптотами.

Ответ: - см. рис. 11 (а) – (в).

Общая схема исследования функции

Пусть – некоторая заданная функция. Требуется провести ее всестороннее (полное) исследование и построить ее график. Указанное полное исследование функции можно провести по следующей схеме.

1. Находим область определения функции. Заодно устанавливаем интервалы ее непрерывности и точки разрыва.

2. Исследуем функцию на четность-нечетность и тем самым устанавливаем возможную симметрию графика функции (относительно оси oy или относительно начала координат). Для этого записываем выражение 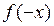и сравниваем его с :

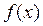а) Если 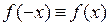, то функция – четная. Ее график симметричен относительно оси оу (рис. 12 (а)).

б) Если 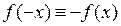, то функция – нечетная. Ее график симметричен относительно начала координат (рис. 12 (б)).

в) Если не имеет место ни вариант (а) ни вариант (б), то функция – общего вида (ее график симметрией (а) и (б) не обладает).

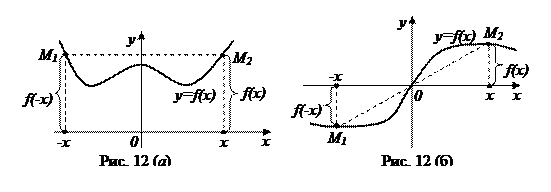
3. Исследуем функцию на периодичность (на повторяемость ее графика). Из элементарных функций это имеет смысл делать лишь для тригонометрических функций, ибо прочие функции заведомо не периодичны.

4. Исследуем поведение функции возле найденных в пункте 1 точек ее разрыва, а также возле границ области ее определения, учитывая при этом информацию, полученную в пунктах 2 и 3. Заодно устанавливаем (определяем) вертикальные и невертикальные асимптоты графика функции.

5. Находим интервалы возрастания и убывания функции и точки ее экстремума (с помощью первой производной 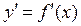). Заодно находим вершины и впадины графика функции и устанавливаем их тип (округлые; острые).

6. Находим интервалы выпуклости и интервалы вогнутости функции и точки ее перегиба (с помощью второй производной 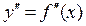). Заодно находим точки перегиба графика функции.

7. Находим точки пересечения графика функции с осями координат.

8. Строим график функции.

Пример 8. Провести полное исследование функции 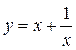и построить ее график.

Решение. Реализуем изложенную выше схему.

1. Область определения функции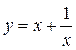– любые x, кроме 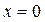. То есть функция определена (а следовательно, и непрерывна) на всей числовой оси ох, кроме точки 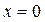, которая, таким образом, является единственной точкой разрыва функции.

2. Исследуем функцию 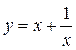на четность-нечетность. Имеем: 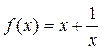; тогда 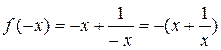. Как видим, 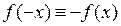. Значит, наша функция – нечетная, ее график симметричен относительно начала координат. А значит, в дальнейшем достаточно исследовать функцию лишь для 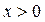, ибо для 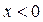можно будет учесть указанную выше симметрию.

3. Функция 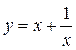– алгебраическая (не тригонометрическая), а следовательно, не периодична.

4. Исследуем поведение функции возле точки ее разрыва 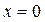(справа, при 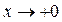), а также при (на правой границе области ее определения):

а) При 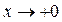функция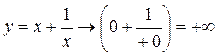

То есть

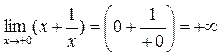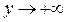(при ).

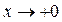А это значит, что вертикальная прямая с уравнением 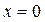(ось оу) является вертикальной асимптотой графика функции. К ней справа (при 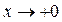) неограниченно приближается график функции, устремляясь при этом вверх (рис. 13 (а)):

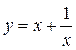б) При функция стремится, очевидно, к 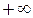, ибо

.

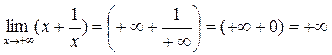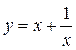При этом, очевидно, при функция стремится к 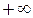эквивалентно функции 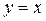, так как 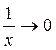при . А это значит, что график нашей функции 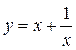при стремится к прямой 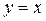. То есть прямая 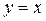– асимптота (наклонная асимптота) графика нашей функции. Причем график функции 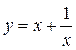при стремится к прямой 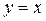сверху, ибо 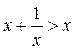для всех 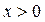(рис. 13 (б)).

5. Найдем интервалы возрастания и убывания и точки экстремума функции (схема исследования изложена выше).

а) Находим производную :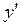

;

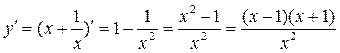б) Найдем точки (значения x), подозрительные на экстремум:

.

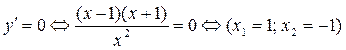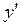не существует .

Точку 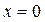исследовать не будем, так как она не входит в область определения функции. Не будем исследовать и отрицательную точку 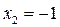(см. пункт 2).

в) Нанесем оставшуюся подозрительную на экстремум точку 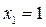на область определения функции (на ось ох). При этом ограничимся рассмотрением лишь положительной полуоси :

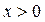В обоих получившихся интервалах найдем знак производной 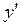и отметим его. Тем самым устанавливаем интервал возрастания 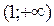и интервал убывания 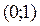функции. Заодно устанавливаем, что 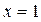– точка минимума функции.

г) Найдем значение функции в точке минимума и тем самым определим впадину графика функции:

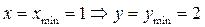; точка 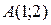– впадина графика функции (округлая, т.к. ).

6. Найдем интервалы выпуклости и интервалы вогнутости функции, а также точки перегиба функции и ее графика (схема исследования изложена выше).

а) Найдем :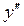

;

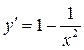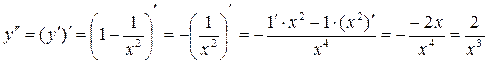
б) Найдем точки (значения x), подозрительные на перегиб:

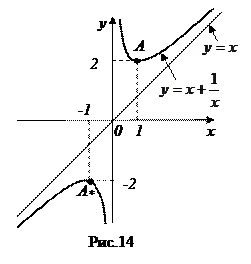
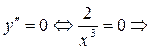таких x нет.

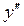не существует .

Но учитывать точку 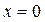не будем, так как она не входит в область определения функции. Итак, рассматриваемая функция не имеет подозрительных на перегиб точек, а значит, точек перегиба у неё нет. И так как для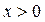 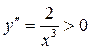, то для всех 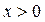функция наша вогнутая.

7. Найдем точки пересечения графика функции с осями координат.

а) С осью ох:

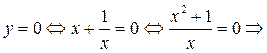таких x нет.

б) С осью оу:

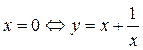– не сущ.

Таким образом, ни с осью ох, ни с осью оу график нашей функции не пересекается.

8. Строим график функции – сначала для 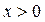, а затем, по симметрии относительно начала координат, и для 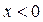(рис. 14).

Дата добавления: 2013-12-13