Гироскопы. Гироскопом называется быстро вращающееся тело, ось вращения которого может изменять свое положение в пространстве

Гироскопом называется быстро вращающееся тело, ось вращения которого может изменять свое положение в пространстве.

Теория гироскопа основана на основном уравнении вращательного движения твердого тела и законе сохранения момента импульса.

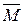d t = = .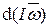

При кратковременных воздействиях даже очень больших сил движение гироскопа практически не изменится.

Гироскопы обладают свойством сохранять направление оси вращения, а также характер сил, действующих со стороны оси тела на опоры при внешних воздействиях.

Если к вращающемуся гироскопу приложить пару сил, стремящихся повернуть его около оси, перпендикулярной к оси его вращения, то он станет поворачиваться около третьей оси, перпендикулярной к первым двум.

Если к гироскопу, вращающемуся относительно оси yy ’приложить пару сил ’, перпендикулярную оси вращения и направленную вдоль оси zz ’, то ось вращения повернется вдоль оси zz ’, верхний конец оси гироскопа в направлении 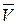,нижний – в направлении 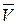’. В результате гироскопического эффекта гироскоп стремится расположить ось своего вращения таким образом, чтобы она образовывала возможно меньший угол с осью вынужденного вращения xx ’ и чтобы оба вращения совершались в одном и том же направлении.

При действии на ось вращения гироскопа пары сил ’ возникает момент сил, направленный вдоль оси xx ’, что приводит к изменению направления вектора момента импульса и повороту оси вращения на угол D j.

Гироскопические силы проявляются и при движении обыкновенного волчка. При наклонном положении вращающегося волчка сила тяжести стремится наклонить его еще больше, но благодаря гироскопическому эффекту ось начинает двигаться. В результате прецессии волчок не падает.

1.4. ДВИЖЕНИЕ ЖИДКОСТИ и газа

(ЭЛЕМЕНТЫ ГИДРО- И АЭРОДИНАМИКИ)

Рассмотрим применение основных законов динамики к простейшим случаям движения жидкости. Под понятием жидкость будем объединять и собственно жидкости (воду, спирт, ртуть и другие тела в жидком агрегатном состоянии), и газы. Общим для обоих случаев является то, что в отличие от твердого тела отдельные частицы жидкости могут перемещаться друг относительно друга, и жидкость, помещенная в какой-либо сосуд, заполняет его и принимает форму сосуда.

Ограничимся простейшим случаем движения жидкости, когда выполняются следующие три условия.

Жидкость несжимаема, т.е. плотность r отдельных движущихся элементов объема жидкости остается во все время движения постоянной.

Для жидкостей подобное приближение вполне естественно, так как их сжимаемость очень невелика. В противоположность жидкостям газы сжимаются легко, и их плотность прямо пропорциональна давлению. Благодаря малому значению плотности для приведения газа в движение достаточно очень малого изменения давления, а следовательно, и плотности газа.

Теория и опыт показывают, что сжимаемостью жидкости или газа можно пренебрегать и с достаточной степенью точности пользоваться понятием несжимаемой жидкости при условии, что скорости их движения малы по сравнению со скоростью распространения звука (v _зв = 333 м/сек).

Понятие несжимаемости характеризует не столько свойства самой жидкости при отсутствии движения, сколько свойства данного движения. И жидкости, и газы при движении практически несжимаемы, когда

v _движ << v _зв

Жидкость идеальна, т.е. отдельные элементы жидкости движутся друг относительно друга без трения. Справедливость подобного пренебрежения трением также зависит от характера изучаемого движения. При движении реальной жидкости или газа внутри нее всегда возникают силы вязкости. Мы будем называть жидкость идеальной тогда, когда во время ее движения можно пренебречь силами внутреннего трения по сравнению с другими силами, действующими в жидкости (силами тяжести, давления и т. п.). В этих случаях потери энергии движения на трение и переход в тепло незначительны и можно применять закон сохранения энергии в чисто механической форме.

Движение жидкости установившееся. Если внешние силы, вызывающие движение жидкости, не зависят от времени, то через некоторое время после начала движения в жидкости установится вполне определенное распределение скоростей. При этом скорость движения каждой частицы жидкости может изменяться от точки к точке вдоль ее траектории. Однако в каждой данной точке пространства скорости движения всех последовательно проходящих через нее частиц жидкости будут одинаковыми. Такое движение жидкости в данной ограниченной части пространства и называется установившимся.

Д.Бернулли вывел соотношение для установившегося движения идеальной несжимаемой жидкости, носящее название уравнения Бернулли.

Для вывода этого уравнения рассмотрим жидкость, движущуюся по трубе переменного сечения. Жидкость втекает слева в сечение 1 площадью S ₁, находящееся на высоте z ₁ над уровнем земли. Скорость втекающих частиц жидкости перпендикулярна к сечению трубы и равна v ₁, давление в жидкости при входе в трубу равно p ₁.

Через сечение 2площадью S ₂, находящееся на высоте h ₂ над уровнем земли, жидкость вытекает из трубы со скоростью v ₂ давление в жидкости на выходе из трубы равно р ₂. Жидкость течет через трубу под действием разности приложенных извне давлений p ₁ – р ₂ или разности уровней h ₁ – h ₂, приводящей к гидростатическому давлению соответствующего столба жидкости, или того и другого вместе.

За бесконечно малый промежуток времени d t через сечение S ₁ втекает масса жидкости d m, заполняющая цилиндрик с площадью основания S ₁и высотой v ₁d t (заштрихованный на рисунке). За тот же промежуток времени через сечение 2 вытечет такая же масса жидкости d m, заполнявшая цилиндрик с площадью основания S ₂ и высотой v ₂d t (также заштрихованный на рисунке). Значение d m можно найти, умножив величину каждого из этих элементарных объемов на плотность жидкости ρ. Тогда получим:

d m = ρ S ₁ v ₁ d t = ρ S ₂ v ₂ d t.

Для несжимаемой жидкости на основании закона сохранения вещества всегда выполняется соотношение, называемое уравнением неразрывности:

ρ S ₁ v ₁ = ρ S ₂ v ₂ или

При перемещении массы жидкости d m по трубе силы внешнего давления совершают работу. Полная сила давления, действующая на левое сечение, равна p ₁ S ₁. Эта сила переместила массу жидкости d m на расстояние v ₁d t. За то же время в правом сечении такаяже масса жидкости d m переместилась на расстояние v ₂d t и совершила работу против силы давления p ₂ S ₂.

Полная работа А сил давления при таком перемещении равна

А = p ₁ S ₁ v ₁ d t – p ₂ S ₂ v ₂ d t

Эта работа затрачена на увеличение кинетической энергии элемента жидкости с массой d m, скорость которого изменилась от v ₁на входе до v₂ на выходе, и на изменение потенциальной энергии этого элемента в поле тяжести при переходе с уровня h ₁на уровень h ₂. Следовательно,

p ₁ S ₁ v ₁ d t – p ₂ S ₂ v ₂ d t = ,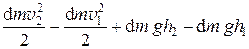

p ₁ – p ₂ = .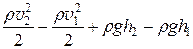

p ₁ + 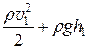= p ₂ +.

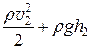Поскольку сечения 1 и 2 могут быть выбраны произвольно, то в любом сечении трубы

p + = const.

Данное уравнение называется уравнением Бернулли и выражает закон сохранения энергии при установившемся движении несжимаемой идеальной жидкости. Это уравнение справедливо для любого движущегося объема жидкости вдоль траектории его движения, называемой линией тока.

Величина 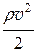представляет собой удельную кинетическую энергию, т.е. кинетическую энергию единицы объема движущейся жидкости. Величина 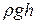есть удельная потенциальная энергия в поле тяжести. Соответственно этому, величина р представляет собой удельную потенциальную энергию сил давления в жидкости.

При движении элементарного объема жидкости происходит непрерывный переход его энергии из одной формы в другую, но полная энергия этого объема остается неизменной.

Так как все члены уравнения Бернулли имеют размерность давления, то это уравнение часто формулируют иначе. Давление р называют статическим напором, величину – гидравлическим напором, а величину 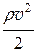– скоростным, или динамическим, напором.

Тогда следует, что полный напор в движущейся жидкости, складывающийся из статического, гидравлического и скоростного напоров, остается постоянным.

Приведем для пояснения два примера.

На рисунке изображена схема водоструйного насоса. Поток воды из водопровода течет по трубке с местным сужением. В узком сечении скорость жидкости резко возрастает и увеличивается скоростной напор 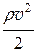. При этом по уравнению Бернулли в суженном сечении падает статический напор и давление р ₂становится ниже атмосферного. Поэтому через отводную трубку в это сечение засасывается воздух из откачиваемого сосуда А. Пройдя суженное сечение, струя воды с воздухом вновь расширяется, ее скоростьпадает, а давление возрастает до атмосферного на выходе из насоса.

Такой насос очень прост по конструкции и может создавать значительное разрежение, понижая давление в откачиваемом сосуде до ~ 10 ^–3 атм.

Работами Д. Бернулли и его современника Эйлера были заложены основы науки о движении жидкостей, выросшей в настоящее время в самостоятельную науку – гидродинамику. Широкое практическое применение гидродинамика получила в конце XIX и начале XX веков в результате работ Н.Е.Жуковского и С.А.Чаплыгина. Ими была создана также новая наука – аэродинамика – учение о законах движения газов и теория полета. Жуковскому первому удалось объяснить механизм подъемной силы, создаваемой крылом аэроплана при движении. На рисунке изображен разрез примерного профиля крыла. Пунктиром показаны линии тока встречного течения воздуха. Как видно из рисунка, над верхней частью крыла происходит сгущение этих линий и увеличение относительной скорости воздушного потока. Согласно уравнению Бернулли давление в потоке над крылом станет меньше, чем под крылом, и за счет этой разности давлений возникает подъемная сила F, удерживающая летящий самолет в воздухе.

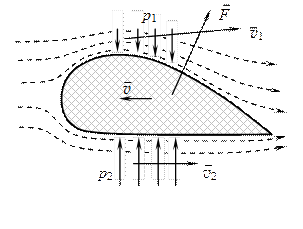На основе этой качественной картины Н.Е.Жуковский разработал количественные методы расчета величины подъемной силы для различных профилей крыла. Созданные им профили, ныне называемые профилями Жуковского, позволили проектировать крылья наивыгоднейшей формы.

При скоростях полета современных скоростных самолетов воздух уже нельзя считать несжимаемой жидкостью. Методы учета сжимаемости воздуха были разработаны С.А.Чаплыгиным еще в 1903 г., когда скорости полета не превышали 30–40 км/час. На основе этих методов рассчитываются подъемная сила и сопротивление крыльев при современных скоростях полета.

1.5. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

Колебательное движение – это движение, при котором тело, выйдя из положения равновесия, периодически возвращается к нему.

Если этот возврат совершается через равные промежутки времени, то колебания называются периодическими колебаниями.

Простейшим случаем периодических колебаний являются гармонические колебания.

1.5.1. Гармонические колебания

Пусть точка D равномерно с угловой скоростью w вращается по окружности радиусом А, тогда угловая координата точки будет меняться согласно уравнению

j = j ₀ + wt,

где j ₀ – значение угла при t = 0.

Проекция точки D на ось 0 х меняется согласно уравнению

х = А cos j = А cos(j ₀ + wt),

проекция точки на ось 0у

у = А sin j = А sin(j ₀ + wt),

j ₀ не влияет на характер движения, а означает лишь изменение начального момента в отсчете времени.

Сos j и sin j являются периодическими функциями от t с периодом

.

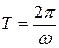Период колебания – промежуток времени, в конце которого точка оказывается в том же положении и движется с той же скоростью, как и в его начале.

Таким образом, точки M и N совершают периодические колебания.

Периодические колебания, при которых смещение меняется по закону sin или cos называются гармоническими колебаниями.

Очевидно, что проекция точки D на любую прямую, и не проходящую через 0, будет совершать гармонические колебания.

В уравнении гармонического колебания х = А cos j = А cos(j ₀ + wt)

А – максимальная величина смещения – амплитуда колебания; j – фаза колебания; j ₀ – начальная фаза колебания; w – угловая скорость вращения точки D – циклическая частота.

Циклическая частота введена в связи с тем, что гармонические колебания – не обязательно проекция движения точки по окружности, например, рассматривая колебания груза на пружине или поплавка в жидкости не удобно описывать такие колебания, пользуясь понятием “угловая скорость”,

Зная уравнение смещения точки при гармоническом колебании

х = А cos j = А cos(j ₀ + wt),

легко найти уравнения изменения других кинематических и динамических характеристик.

Скорость движения точки

v = = – wА sin j = – wА sin(j ₀ + wt).

Ускорение движения точки

a = = 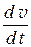– w ² А cos j =

= – w ² А cos(j ₀ + wt)

или a = – w ² х.

Из полученных уравнений и их графического представления следует:

– смещение х, скорость v, ускорение а точки меняются гармонически с одинаковой циклической частотой w и периодом Т;

– амплитуда колебаний | х _max | = | A |, | v _max| = | ωА |, | a _max| = | Aω ²|;

– фазы колебаний различны:

– колебания скорости опережают колебания смещения на 0,5 p,

– колебания ускорения опережают колебания смещения на p.

Например, при прохождении положения равновесия х = 0 и возрастает, v = v _max , а = 0 и убывает.

Сила, действующая на точку

F = ma = – m w ² А cos(j ₀ + wt) = – m w ² х

или F = – m w ² х,

т.е. направление силы противоположно направлению смещения, т.е. сила всегда направлена к положению равновесия.

Из выше изложенного следует

ma = – m w ² х,

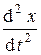= – w ² х,

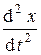+ w ² х = 0

последнее уравнение является дифференциальным уравнением гармонических колебаний.

Кинетическая энергия колеблющейся точки

Е _к = mv ² = m w ² А ²sin² (j ₀ + wt).

Потенциальная энергия точки, колеблющейся под действием упругих сил

Е _р = 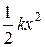= m w ² А ²cos²(j ₀ + wt).

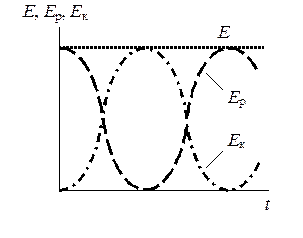Полная энергия колеблющейся точки

Е = Е _к + Е _р = m w ² А ²sin²(j ₀ + wt) + m w ² А ²cos²(j ₀ + wt) = m w ² А ².

Е = Е _{к max} = Е _{р max}

Дата добавления: 2013-12-13