Определение касательных напряжений при поперечном изгибе

При поперечном изгибе наряду с изгибающим моментом в сечении балки возникает поперечная сила (Q). Наличие поперечной силы связано с возникновением в поперечном сечении касательных напряжений.

Русский инженер – мостостроитель Дмитрий Иванович Журавский в связи с проектированием деревянных мостов для ж/д Петербург – Москва проводил исследования определения и изменения касательных напряжений при поперечном изгибе и разработал в 1844-1850гг. теорию касательных напряжений в балках прямоугольного профиля. Им было установлено, что касательное напряжение при изгибе не распределяются равномерно на высоте сечения. Также он получил формулу для подсчета касательных напряжений при изгибе, которая носит название формулы Журавского.

τ =

Q_y (Q) – поперечная сила в рассматриваемом сечении.

S`_x – статистический момент относительно нейтральной оси той части сечения, которая лежит выше или ниже прямой проведенной через данную точку;

I_x – осевой момент инерции всего сечения относительно нейтральной оси.

b – ширина поперечного сечения на уровне точки, в которой определяется напряжение.

Q, I_x, b для сечения постоянной ширины не меняются.

S_x изменяется в зависимости от y₁ следовательно τ в любой точке поперечного сечения зависит только от y₁. Касательные напряжения достигают максимального значения:

Для прямоугольного сечения: τ_max =

в точках на нейтральной линии, т. е. при y = 0.

Для двутавра: τ_max = 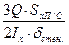, где S_xП/С – статистический момент полусечения.

Для круглого сечения: τ_max = , где A – площадь.

Максимальное касательное напряжение для большинства симметричных сечений относительно нейтральной оси (X) имеет место в точках лежащих на нейтральной оси.

Для стальных балок [τ] ≈ 0,6∙ [σ]

Условие прочности по касательным напряжениям: τ_max ≤ [τ]

Дата добавления: 2013-12-13