Элементы специальной теории относительности

Работа консервативных (потенциальных) сил при элементарном изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, таккак работа совершается за счет убыли потенциальной энергии: dA = -dW

Потенциальное поле сил.

Потенциальное поле - поле, в котором работа, совершаемая силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Силы, действующие в таких полях, называются консервативными (например, сила тяготения). Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной (например, сила трения).

Поскольку 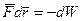, то 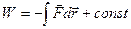, отсюда F = -gradW =-∆V,

где вектор gradW =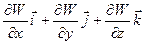 называется градиентом скаляра W и обозначается 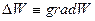. Символ 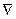("набла") обозначает символический вектор, называемый опeратором Гамильтона или набла-оператором:

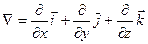
Конкретный вид функции W зависит от характера силового поля.

1)Потенциальная энергия тела массы т на высоте h:

2) Потенциальная энергия упругодеформированного тела.

35. Поле сил тяготения.

Закон всемирного тяготения Между любыми двумя материальными
точками действует сила взаимного притяжения, прямо _{т т}

9 пропорциональная произведению масс этих точек и обратно F = G —^~-
(пропорциональная квадрату расстояния между ними: ^г

где G = 6.67 10~" Н-м² кг~² — гравитационная постоянная.

Эта сила называется гравитационной, или силой всемирного тяготения. Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела.

Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения, или гравитационного поля.

На примере гравитационного поля рассмотрим понятия напряженности поля и потенциала поля.

Напряженность поля тяготения это физическая величина, равная отношению силы, действующей со стороны поля на помещенное в него тело (материальную точку), к массе этого тела.

Напряженность является векторной силовой характеристикой поля тяготения.

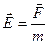
В гравитационном поле Земли 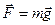, откуда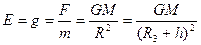

где R₃ - радиус Земли, масса которой М, h - расстояние от центра тяжести тела до поверхности Земли. При перемещении тела массой т на расстояние dR поле тяготения совершает работу dA= (знак минус потому, что сила и перемещение противонаправлены).

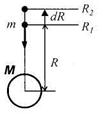При перемещении тела с расстояния R₁, до расстояния R₂:

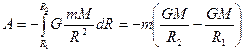
Работа не зависит от траектории перемещения, а определяется только начальным и конечным положениями тела.

Следовательно, силы тяготения консервативны, а поле тяготения является потенциальным. Работа консервативных сил равна изменению потенциальной энергии системы с обратным знаком. А=-(W₂ –W₁). Поэтому,

потенциальная энергия поля сил тяготения: W =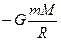

Для любого потенциального поля можно определить скалярную энергетическую характеристику поля - потенциал.

Потенциалом поля тяготения в данной точке поля называется скалярная величина, равная отношению - потенциальной энергии материальной точки, помещенной в рассматриваемую точку поля, к массе материальной точки:

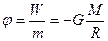
Рассмотрим связь между потенциалом поля тяготения и его напряженностью:

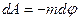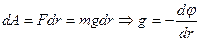, или

В общем случае для любого потенциального поля между напряженностью и потенциалом существует связь:

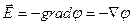
Эта формула является следствием соотношения 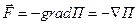. Знак минус указывает на то, что вектор напряженности направлен в сторону убывания потенциала.

36. Космические скорости.

Первой космической скоростью называют такую минимальную скорость, которую надо сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, т.е. превратиться в искусственный спутник Земли.

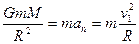(2-ой закон Ньютона); 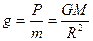(R- радиус Земли)

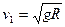= 7,9 км/с (у поверхности Земли (h → 0))

Второй космической скоростью называется наименьшая скорость, которую надо сообщить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спутник Солнца. В этом случае кинетическая энергия тела должна быть равна работе, совершаемой против сил тяготения:

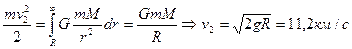
Третьей космической скоростью называется скорость, которую необходимо сообщить телу на Земле, чтобы оно покинуло пределы Солнечной системы, преодолев притяжение Солнца: v₃ = 16,7 км/с.

37. Преобразования Галилея

В классической механике, при скоростях тел значительно меньших, чем скорость света (v «с), справедлив механический принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета.

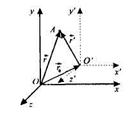
Рассмотрим две системы отсчета: инерциальную систему К (с координатами х,у,z), которую будем считать неподвижной, и систему К' (с координатами х',у',:'), движущуюся относительно К равномерно и прямолинейно с постоянной скоростью 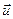= const.

В начальный момент времени начала координат О и О' этих систем совпадают.

В произвольный момент времени t: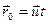

Для произвольной точки А: 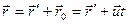. Или в проекциях на оси координат:

Дата добавления: 2013-12-13