Кинетическая энергия: К=Е-Ео=т0с2

X = x' + uxt, y = y' + uуt, z = z' + uzt.

Эти соотношения называются преобразованиями координат Галилея.

Продифференцировав их по времени получим правилосложения скоростей в классической механике: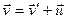

В классической механике предполагается, что ход времени не зависит от
относительного движения систем отсчета, поэтому к преобразованиям Галилея
можно добавить еще одно соотношение: t = t'

Ускорение в системах отсчета, движущихся относительно друг друга равномерно и прямолинейно, одинаково:

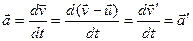
Это и служит доказательством принципа относительности Галилея.

38. Постулаты Эйнштейна.

1) Принцип относительности: никакие опыты, проведенные внутри данной
инерциальной системы отсчета, не дают возможность обнаружить, покоится ли
эта система или движется равномерно и прямолинейно; все законы природы
инвариантны по отношению к переходу от одной системы отсчета к другой.

2) Принцип инвариантности скорости света: скорость света в вакууме
не зависит от скорости движения источника света или наблюдателя и
одинакова во всех инерциальных системах отсчета.

39. Преобразования Лоренца.

Пусть система О' движется относительно системы O со скоростью
v= const, причем (с - скорость света (скорость распространения
электромагнитных взаимодействий) в вакууме). Обозначим отношение
скоростей v и с через 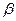=v/c. Пусть вектор скорости 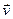направлен вдоль оси ОХ. Тогда релятивистские преобразования координат и времени будут иметь вид: .

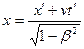Эти соотношения - преобразования Лоренца - при v«c переходят в преобразования Галилея.

у = у', z = z',

Они устанавливают взаимосвязь пространства и времени -в закон преобразования координат входит время, а в закон преобразования времени — пространственные координаты.

;

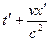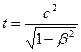
Следствием этого является тот факт, что если два события в системе О происходят одновременно но в разных точках (t₁=t₂, x_l ≠х₂), то в системе О' эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.

Пусть в некоторой точке х в системе О происходит событие длительностью τ = t₂ – t₁, то в системе О' длительность этого же события

Т.о. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.

Рассмотрим стержень, расположенный вдоль оси х' и покоящийся относительно системы О'. Его длина в системе О' будет 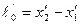. Чтобы определить длину 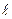= х₂ – х₁, этого стержня в системе O, относительно которой он движется со скоростью v, измерим координаты его концов х₁, и х₂ в один и тот де момент времени t.

Размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения, причем лоренцово сокращение длины тем больше, чем больше скорость движения. Поперечные размеры тел не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.

Если материальная точка движется в системе О' вдоль оси х' со скоростью , а сама система О' движется со скоростью и относительно системы О, то релятивистский закон сложения скоростей:

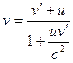
В качестве величины, инвариантной по отношению к преобразованию координат в четырехмерном пространстве Эйнштейна (не зависящей от выбора системы отсчета) вводится интервал между событиями:

,

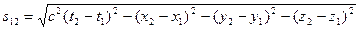где - расстояние между точками обычного трехмерного пространства. Обозначив t₁₂ =t₂ –t₁, получим

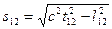
40. Основные соотношения релятивистской динамики

Релятивистская масса т движущихся релятивистских частиц (тел)зависит от их скорости.

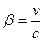
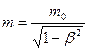
т₀ - масса покоя частицы, т.е. масса, измеренная в той инерциальной cистеме отсчета, в которой частица находится в покое.

Релятивистский импульс 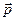. Релятивистский импульс системы cохраняется. Закон сохранения релятивистского импульса - следствие однородности пространства.

Основной закон релятивистской динамики:

Законы классической динамики получаются из законов релятивистской динамики в предельном случае v «с (или с→∞). Т.о. классическая механика - это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).

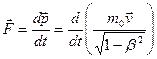
Полная энергия тела массы т: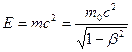

Соотношение Е = тс² носит универсальный характер, оно применимо ко всем формам энергии, т.е. можно утверждать, что с энергией, какой бы формы она не была, связана масса т=Е/с² и, наоборот, со всякой массой связана энергия. Покоящееся тело обладает энергией: Е_о=т_ос, называемой энергией покоя.

Полная энергия замкнутой системы сохраняется. Закон сохранения энергии - следствие однородности времени

Релятивистское соотношение между полной энергией и импульсом тела:

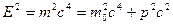
Величина Е² - р²с² = является инвариантом системы.

В случае, когда масса покоя частицы равна нулю, то Е²-с²р²=0. Следовательно, такая частица может обладать отличными от нуля энергией и импульсом только в том случае, когда она движется со скоростью света. К таким частицам относятся фотоны.

Основной вывод теории относительности - пространство и время органически взаимосвязаны и образуют единую форму существования материи - пространство-время.

Дата добавления: 2013-12-13