Броуновское движение

Явления диффузии, теплопроводности, вязкого трения обусловлены взаимодействием молекул в газе и проявляются в случае, когда длина свободного пробега молекул много меньше характерных размеров протекающих процессов.

Примеры процессов переноса.

1) Диффузия – это процесс самопроизвольного выравнивания концентраций веществ в смесях.

Например, в смеси двух газов условие отсутствия перемешивания состоит в том, что суммарное давление постоянно. По закону Дальтона: 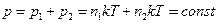, поэтому для концентрации: 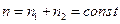. Введем физическую величину – относительную концентрацию молекул одного из газов 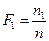, тогда для плотности потока относительной концентрации имеем

.

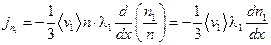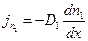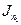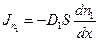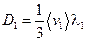Это уравнение называют уравнением диффузии. Пусть , тогда выражение для потока частиц примет вид: , где - коэффициент диффузии. Аналогичные выражения можно записать и для второго газа, имеющего концентрацию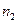. Если m ₁ – масса молекулы, то плотность газа 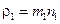, поэтому, умножая обе части последнего уравнения на m ₁, для потока плотности (или потока массы) получаем уравнение

,

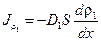которое называется первым законом Фика.

2) Теплопроводность – процесс выравнивания температуры в различных точках среды. Молекулы газа, находясь в постоянном хаотическом движении, при упругих соударениях обмениваются кинетической энергией поступательного движения, что приводит к выравниванию температуры. Введем физическую величину - энергия теплового движения молекулы газа, где i – число степеней свободы молекулы, а температура Т зависит только от координаты x. Тогда уравнение переноса для плотности потока физической величины Q примет вид:

.

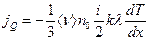
Это уравнение называют уравнением теплопроводности. Но 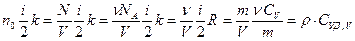, поэтому .

Если ввести обозначение 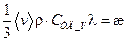- коэффициент теплопроводности, то плотность потока теплоты можно записать в виде: 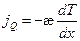, а для потока теплоты 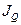через площадку площадью S, перпендикулярную оси OX, соответственно получим: .

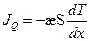3) Вязкость (внутреннее трение) приводит к появлению силы сопротивления при движении тела в жидкости или газе. Вязкость вызвана переносом импульса молекулами (при их хаотическом движении) между слоями газа (жидкости), скорость которых неодинакова. В частности, это можно наблюдать в следующем опыте. Пусть две одинаковые тонкие достаточно длинные пластинки расположены в газе параллельно друг другу на расстоянии h. Если одна из них движется относительно другой с небольшой по величине скоростью u, то на каждую из пластин будет действовать сила трения, величина которой

.

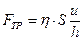Параметр h называется коэффициентом вязкости.

Для вывода уравнения вязкости, надо рассмотреть поток газа вдоль горизонтальной оси Y, скорость которого меняется в поперечном направлении X. Молекулы в газе движутся хаотически, но у каждой из них можно выделить некоторую среднюю скорость, равную скорости газа u. В качестве физической величины F рассмотрим импульс молекул газа 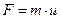. Тогда

плотность потока импульса: 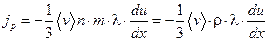- уравнение вязкости, а

поток импульса: .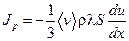

С учетом равенства 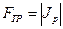, считая приближенно 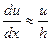в случае h >l, получаем выражение для коэффициента вязкости . Поэтому

, .

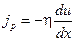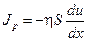Замечание. Между коэффициентами переноса существует зависимость

.

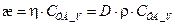При увеличении длины свободного пробега молекул все более значимыми становятся явления, связанные со свойствами самих молекул, так как процессы столкновения играют меньшую роль.

Состояние газа, при котором длина свободного пробега молекул l сравнима с размерами сосуда L, в котором находится газ, называется вакуумом. Различают низкий вакуум l<<L, средний l~L и высокий (глубокий) вакуум l>>L.

Замечание. В определении вакуума важен размер сосуда, например, для воздуха в обычных условиях 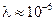м, поэтому в любой микроцарапине или микротрещине газ будет находиться в состоянии среднего вакуума.

Эффузия – это явление медленного истечения газа из малого отверстия. Различают эффузию двух видов. В первом случае размер отверстия много меньше длины свободного пробега молекул – эффузия в разреженном газе. Во втором случае давление газа в сосуде настолько велико, что истечение газа достаточно точно описывается уравнениями гидродинамики.

Эффузия в разреженном газе.

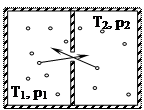Так как в этом случае длина свободного пробега много больше размера отверстия, то процессы столкновения молекул играют незначительную роль, поэтому истечение становится молекулярным.

Рассмотрим сосуд с газом, в котором есть перегородка с отверстием, меньшим по размеру, чем длина свободного пробега молекул в сосуде. Пусть левая часть находится при постоянной температуре Т₁, а правая при Т₂. Суммарная плотность потока молекул через отверстие

.

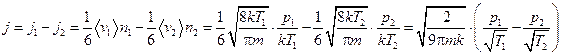Предположим, что в начале процесса давления газа с обеих сторон были одинаковыми, но температуры разными, тогда поток молекул будет направлен в сторону части с большей температурой – это явление носит название тепловой эффузии.

При равновесии суммарный поток 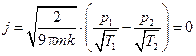, поэтому .

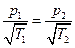Как видно, условие равновесия для разреженного газа не является равенством давлений.

Из формулы для плотности потока 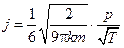следует, что молекулы с большей массой в меньшем количестве проходят через отверстие, чем молекулы с меньшей массой. Таким образом, если в сосуде находится смесь газов, то возможно разделение смеси газов, находящихся при одинаковой температуре – изотермическая эффузия.

Броуновское движение (иногда называют Брауновское движение) – беспорядочное движение малых частиц, взвешенных в жидкости или газе, происходящее под действием молекул окружающей среды. Исследовано в 1827 г. Броуном (Браун; Brown), который наблюдал в микроскоп движение цветочной пыльцы, взвешенной в воде.

Частицы размером около 1 мкм и менее совершают неупорядоченные независимые движения, описывая сложные зигзагообразные траектории. Интенсивность броуновского движения не зависит от времени, но возрастает с увеличением температуры, уменьшением вязкости и размеров частиц (независимо от их химической природы.)

Теория броуновского движения была построена независимо друг от друга Эйнштейном и Смолуховским в 1905-1906 гг. Причиной броуновского движения является тепловое движение молекул среды, проявляющееся в некомпенсированных ударах молекул о частицу, т.е. в флуктуациях давления. Эти удары приводят частицу в беспорядочное движение. Если отмечать положения частицы через равные небольшие промежутки времени, то траектория окажется сложной и запутанной.

Как показывают опытные данные, квадрат смещения частицы из начального положения в проекции на любую ось: 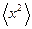за время наблюдения t, в отсутствие внешних сил определяется выражением 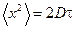, где коэффициент диффузии броуновской (сферической) частицы , a – радиус частицы, h - коэффициент вязкости.

При описании броуновского движения частицы в одномерном случае можно считать, что на частицу действует случайная сила, среднее значение которой равно нулю, 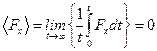и сила сопротивления 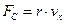, где r – коэффициент вязкого трения броуновской частицы в жидкости. Уравнение движения 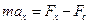при подстановке выражения для силы сопротивления примет вид

.

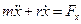Умножим это уравнение на x и используем равенство 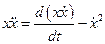, тогда получим:

.

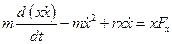Проведём усреднение по времени

.

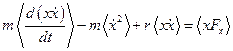Тогда 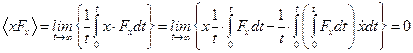. Для одномерного движения по теореме о распределении энергии по степеням свободы: .

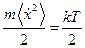Заменяем 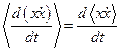и получаем уравнение 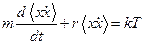, откуда

.

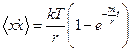Для установившегося движения 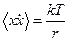. Так как 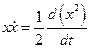, то 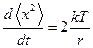. После интегрирования по времени получаем 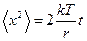. Для сферической броуновской частицы, радиус которой равен a, имеем: 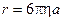, поэтому .

Полученные выше формулы были экспериментально проверены в 1908 году Перреном, который измерял с помощью микроскопа перемещения броуновских частиц за одинаковые промежутки времени. Ему удалось на основании своих опытов с помощью этих формул определить постоянную Больцмана k и вычислить значение постоянной Авогадро N _A, совпадающие по величине с их значениями, полученными другими методами.

Замечание. Теория броуновского движения нашла широкое применение не только для описания случайного движения частицы в жидкости, но и для решения целого ряда прикладных задач. Этой теории подчиняются случайные тепловые колебания высокоточных механических и электрических измерительных устройств, таких, например, как крутильные весы и гальванометры. Кинетические уравнения, полученные в теории броуновского движения, используются для анализа точности работы различных систем управления. Они позволяют рассчитать случайные ошибки, возникающие при управлении техническими устройствами и провести оптимизацию их параметров.

Дата добавления: 2013-12-13