Плоскость в пространстве

Уравнения поверхностей и линий

Уравнением поверхности называется такое уравнение, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и не удовлетворяют координаты любой точки, не лежащей на ней:

F (x, y, z) = 0.

Геометрическим образом этой зависимости служит поверхность.

Одну из координат в этом уравнении, например z, можно рассматривать как неявную функцию двух других.

Возможно другое, параметрическое выражение функциональной зависимости между несколькими переменными с помощью вспомогательных переменных – параметров. Так, чтобы определить положение точки на поверхности, нужны два параметра, например широта и долгота на поверхности шара. Тогда говорят, что поверхность задана параметрически.

Если уравнения F ₁(x, y, z) = 0 и F ₂(x, y, z) = 0 являются уравнениями двух поверхностей, пересекающихся по линии L, то линия L есть геометрическое место общих точек этих поверхностей, координаты которых удовлетворяют системе уравнений:

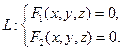
В случае двух переменных зависимость между ними 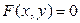может быть геометрически истолкована как уравнение плоской кривой. Любую величину t,

определяющую положение точки (x, y) на этой кривой, можно принять за параметр. Тогда 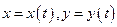дадут параметрические уравнения кривой.

Плоскость – одно из исходных понятий геометрии, определяется аксиомами.

Характеризуется свойствами:

1) плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;

2) плоскость есть множество точек, равноотстоящих от двух заданных точек.

Для решения задач аналитической геометрии используют различные, наиболее подходящие к каждому случаю виды уравнений плоскости.

Дата добавления: 2013-12-13