Изменение начала координат и поворот осей

Поворот координатных осей

Выведем формулу преобразования координат при повороте координатных осей.

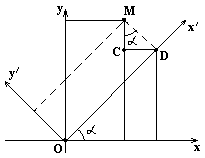
Повернём оси координат на угол a относительно исходной системы координат. Координаты точки М в системе координат x¢Oy¢ равны x¢ и y¢. Найдём её координаты в системе коорднат xOy. В треугольнике CMD 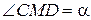, OD=x¢, MD=y¢.

Следовательно, x=OA=OB-AB=OB-CD, y=MA=AC+CM=DB+CM.

Поскольку

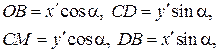
то 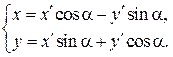(3)

Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x¢,y¢) этой же точки при повороте осей на угол a.

Формулы, выражающие новые координаты (x¢,y¢) точки М через её старые координаты (x,y), получим из следующих соображений: если новая система получена поворотом старой на угол a, то старая система получается поворотом новой на угол (-a), поэтому в равенствах (3) можно поменять местами старые и новые координаты, заменяя одновременно a на (-a).

Выполнив это преобразование, получим

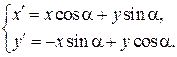
Если оси декартовой прямоугольной системы переносятся параллельно на величины x₀ по оси ox и на y₀ по оси oy и, кроме того, поворачиваются на угол a, то этому изменению системы соответствуют формулы преобразования координат, выражающие старые координаты через новые

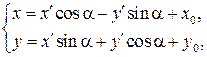(4)

и новые координаты через старые:

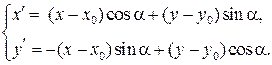(5)

Приведение общего уравнения кривой второго порядка
к каноническому виду

Пусть кривая второго порядка задана в общем виде:

.

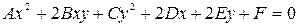Всякая линия второго порядка есть либо эллипс, либо парабола, либо распадается на пару прямых (пересекающихся, параллельных или совпадающих).

Приведение этого уравнения к каноническому виду заключается в нахождении системы координат, в которой кривая имеет канонический вид, геометрически это может быть достигнуто поворотом координатных осей на угол, совмещающий оси симметрии кривой с координатными осями и переносом начала координат в центр кривой (x ₀ ,y ₀).

1) Члены, содержащие переменные в первой степени, исчезают после выделения в общем уравнении полных квадратов, тем самым алгебраически позволяют найти центр кривой после применения формул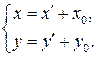

Центр кривой, если он существует, находится из системы

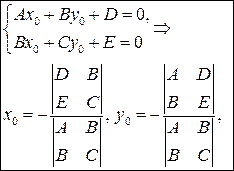(6)

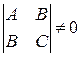– условие центральности.

Кривые второго порядка, имеющие единственный центр, называются центральными.

После переноса начала координат в центр (x ₀ ,y ₀) уравнение кривой примет вид

,

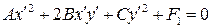где .

2) Члены, содержащие произведение текущих координат исчезают после

применения формул

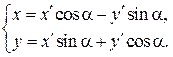
подвергнем уравнение (6) преобразованию поворота осей координат на угол .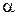

После преобразования

где 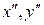- новые координаты.

Выпишем из преобразованного уравнения, слагаемые второго порядка:

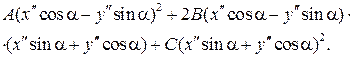
Из этих слагаемых нас интересует слагаемое, содержащее произведение 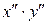, коэффициент перед которым равен

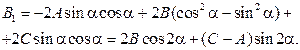
Угол поворота находится из условия В₁=0: .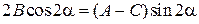

Откуда 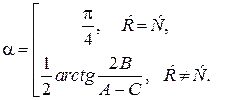(7)

Каноническое уравнение кривой принимает вид:

,

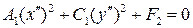где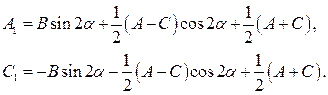

Сделаем некоторые замечания о виде линий второго порядка.

При переходе от одной системы прямоугольных координат к другой мы заменяем уравнение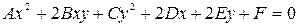

линии второго порядка другим уравнением

.

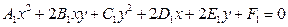При этом выражения 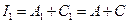и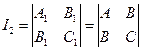

остаются равными. Они называются инвариантами (неизменными) уравнения второй степени.

С их помощью различают три типа линий второго порядка.

1) Эллиптический тип, если .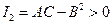

К нему относятся, кроме действительного эллипса, также мнимый эллипс

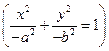
и пара мнимых прямых, пересекающихся в действительной точке .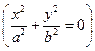

2) Гиперболический тип, если .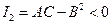

К нему относится, кроме гиперболы, пара действительных пересекающихся прямых .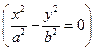

3) Параболический тип, если .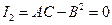

К нему относится, кроме параболы, пара параллельных (действительных или мнимых) прямых (они могут совпадать).

Пример. Приведите уравнение 5 x ² + 9 y ² – 30 x + 18 y + 9 = 0 к каноническому виду и постройте кривую.

Выделим полный квадрат: сгруппируем члены этого уравнения, содержащие одноименные координаты:
(5 x ² – 30 x) + (9 y ² + 18 y) +9 = 0, 5 (x ² – 6 x) + 9(y ² + 2 y) +9 = 0.

Дополним члены в скобках до полных квадратов:
5(x ² – 6 x + 9 – 9) + 9(y ² + 2 y + 1 – 1) + 9 = 0, 5(x – 3)² + 9(y + 1)² = 45.

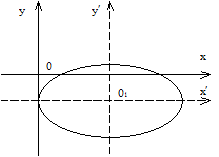
Введем новые координаты: x¢ = x – 3, y¢ = y + 1, x ₀ = 3, y ₀ = -1,

то есть точка О ₁(3, -1) – центр кривой.

Уравнение в новой системе координат принимает вид:

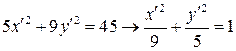, определяет эллипс с полуосями а =3, b= 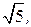который в исходной системе координат имеет центр в точке О₁(3, -1).

Пример. Определите вид кривой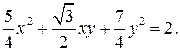

Определим угол поворота осей по формуле (7):

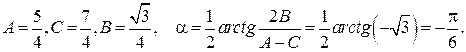
Подвергнем уравнение кривой преобразованию:

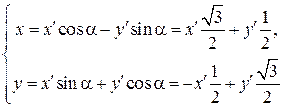
и получим уравнение эллипса

.

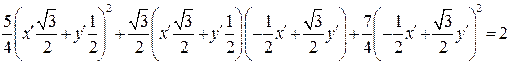x¢ ² + 2 y¢ ² = 2.

Дата добавления: 2013-12-13