Формулы для коэффициентов переноса в случае идеального газа

Рассмотрим вывод формул для коэффициентов переноса в случае идеального газа.

1. Средняя длина свободного пробега молекул газа. Молекулы идеального газа непрерывно хаотически движутся, сталкиваясь друг с другом. От одного столкновения до другого они движутся по прямой линии, а их общая траектория представляет собой ломаную линию, состоящую из прямолинейных участков

Рис. 2.16

(рис. 2.16,а). Под средней длиной свободного пробега понимают величину, равную пути, пройденному молекулой за время , деленному на число столкновений 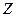, которое испытала молекула за это время

.

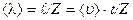Выведем формулу для средней длины свободного пробега. Будем считать, что все молекулы неподвижны, кроме одной молекулы. За время молекула пройдет расстояни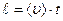е , где 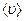- средняя арифметическая скорость молекулы. Причем она за это время испытает столкновения со всеми молекулами, центры которых попадают внутрь коленчатого цилиндра (его радиус равен диаметру одной молекулы, а длина образующей цилиндра равна пройденному молекулой расстоянию 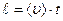, рис. 2.16,а). Число столкновений движущейся молекулы будет равно количеству молекул, центры которых попали в этот цилиндр

,

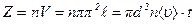что позволяет записать

, (2.77)

где в формулу (2.77) введен коэффициент , учитывающий движения всех молекул - в этом случае нужно для определения числа столкновений 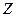использовать относительную скорость молекул, а не скорость молекул относительно стенки сосуда. Это приводит к следующим формулам:

,

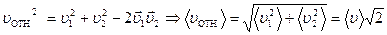где учтено, что усреднение слагаемого по всевозможным углам 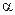() дает нулевое значение ().

Дата добавления: 2013-12-13