Биссекторные плоскости

Комплексный чертеж (эпюр Монжа)

Точка

Методы проецирования, представленные в § 1.1, позволяют строить изображения (проекции) по заданному геометрическому образу (оригиналу), т.е. решать прямую задачу начертательной геометрии. Но в ряде случаев предусматривается решение обратной задачи, которая заключается в построении оригинала в пространстве по его проекциям на плоскости проекций.

Таким образом, приведенные выше проекционные чертежи (см. рис. 3, рис. 6, рис. 7, рис. 9) не позволяют восстановить оригинал, т.е. не обладают свойством «обратимости».

Рассмотрим схему построения обратимого чертежа, используемую в начертательной геометрии.

Ортогональное проецирование является частным случаем параллельного проецирования, когда направление проецирования перпендикулярно (ортогонально) плоскости проекций: S ^ П_i.

Ортогональное проецирование является основным в черчении, т.к. обладает большой наглядностью и позволяет при определенном расположении геометрических образов относительно плоскостей проекций сохранить ряд линейных и угловых параметров оригинала.

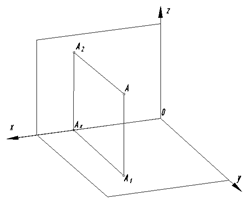
Французский геометр Гаспар Монж предложил ортогонально проецировать оригинал на две взаимно перпендикулярные плоскости проекций П₁ и П₂.

X

Рис. 11 Рис. 12

П₁ – горизонтальная плоскость проекций; П₂ - фронтальная плоскость проекций; х = П₁ Ⴖ П₂.

Плоскости проекций разделяют пространство на четыре четверти (или квадранты). Четверти нумеруются в порядке, указанном на рис. 11. Система координат выбрана из условия совпадения координатных плоскостей с плоскостями проекций. На рис. 12 показано проецирование точки А на плоскости П₁ и П₂ . Проецирующие лучи АА ₁ и АА ₂ перпендикулярны соответствующим плоскостям проекций, поэтому фронтальная (А₂) и горизонтальная (А₁) проекции точки А находятся на перпендикулярах А₁А_х и А₂А_х к оси проекций х.

Повернув плоскость проекций П₁ вокруг оси х на угол 90⁰ (рис. 13), получим одну плоскость – плоскость чертежа, проекции А₁ и А₂ расположатся на одном перпендикуляре к оси проекций х – линии связи. В результате совмещения плоскостей проекций П₁ и П₂ получается чертеж, называемый эпюром Монжа. Эпюр Монжа называют в современной литературе еще комплексным чертежом. Это чертеж состоящий из двух и более связанных между собой проекций геометрического образа. В дальнейшем эпюр Монжа будем называть одним словом – чертеж.

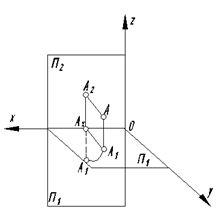
Рис. 13 Рис. 14

Так как плоскости проекций безграничны, то чертеж точки А в системе П₁/П₂ будет выглядеть так, как на рис. 14.

А₂А_х – расстояние от точки А до плоскости проекций П₁;

А₁А_х – расстояние от точки А до плоскости проекций П₂.

Поэтому проекции точки А на две плоскости проекций полностью определяют ее положение в пространстве.

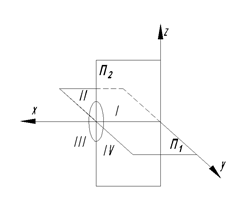
Для упрощения дальнейших рассуждений будем рассматривать лишь часть пространства, расположенную влево от профильной плоскости проекции П₃.

П₃ – профильная плоскость проекций; Z = П₂ Ⴖ П₃; Z – ось ординат. Плоскость проекции П₃ перпендикулярна к П₁П₂.

На рис. 15 показано направление поворота на угол 90⁰ плоскостей проекций П₃ и П₁ вокруг соответствующих осей координат до совмещения с П₂ .

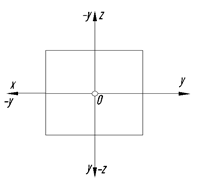
Из рис. 15 видим, что ось Х делит горизонтальную плоскость проекций П₁ на две части: переднюю полу П₁ (оси Х и Y) и заднюю полу П₁ (оси Х и Y).

Ось абсцисс Х делит фронтальную плоскость проекций П₂ также на две части: верхнюю полу П₂ (оси Х и Z) и нижнюю полу (оси Х и -Z).

Рис. 15    

Оси ординат Y и аппликат Z делят профильную плоскость П₃ на четыре части: верхнюю переднюю полу П₃ (оси Z и Y); верхнюю заднюю полу П₃ (оси Z и –Y); нижнюю переднюю полу П₃ (оси -Z и Y); нижнюю заднюю полу П₃ (оси -Z и –Y).

На рис. 16 показан совмещенный комплексный чертеж трех плоскостей проекций

Координата	Четверть пространства
I	II	III	IV
х	+	+	+	+
у	+	-	-	+
z	+	+	-	-

Таблица  

	Рис. 16

Из рис. 15 видно, что точки, расположенные в различных четвертях пространства, имеют определенные знаки координат. Эти знаки приведены в таблице.

Построение проекций точки А в системе П₁/П₂/П₃ показано на рис. 17

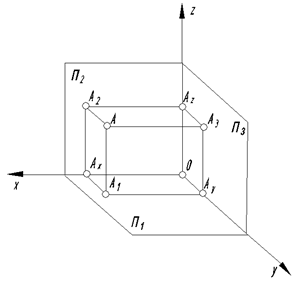
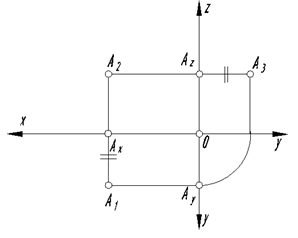
Рис. 17 Рис. 18

ОА_х – удаление точки А от профильной плоскости проекций;

А₃ – профильная проекция точки А;

А₁А_х А₂, А₂А_zА₃ – линии связи.

На чертеже фронтальная и профильная проекции точки лежат на одной линии связи, перпендикулярной к оси Z, причем профильная проекция находится на таком же расстоянии от оси Z, что и горизонтальная от оси Х: А_zА₃ = А_хА₁.

Горизонтальная проекция точки А₁ определяется координатами Х и Y

фронтальная А₂ – координатами Х и Z, профильная П₃ – координатами Y и Z.

Относительно плоскостей проекций точка может занимать следующие положения:

1. Точка располагается в какой-либо четверти пространства, при этом обязательно условие, что Х ≠ 0; Y ≠ 0; Z ¹ 0.
2. Точка принадлежит какой-либо плоскости проекций, при условии, что одна из координат должна быть равна «0».

А Î П₁, если Ζ = 0;

А Î П₂, если Y = 0;

А Î П₃, если Х = 0.

3. Точка принадлежит оси координат, если две любые координаты будут равны «0».

А Î Х, если Y = 0; Z = 0;

А Î U, если Х = 0; Z = 0;

А Î Z, если Х = 0; Y = 0.

Биссекторная плоскость – осевая плоскость, проходящая через ось проекций Х и расположенная под углом 45⁰ к плоскостям проекций П₁ и П₂. Существует две биссекторные плоскости: первая проходит через первую и третью четверти пространства, вторая – через вторую и четвертую четверти пространства. Если точка принадлежит биссекторной плоскости, то численные значения координат Y и Z должны быть равны.

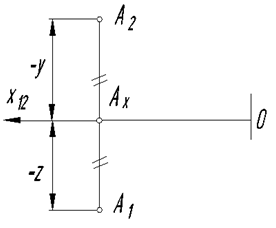
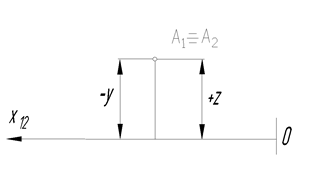
Рис. 19 Рис. 20

На рис. 19 показан чертеж точки А, принадлежащей первой биссекторной плоскости и расположенной в третьей четверти пространства.

На рис. 20 показан чертеж точки А, принадлежащей второй биссекторной плоскости и расположенной во второй четверти пространства.

Контрольные задания по теме «Точка»

	Ответ
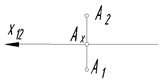1. Какой отрезок на эпюре определяет удаление точки А от горизонтальной плоскости проекций?	A1Ax Oax A2Ax
2. По координатам точки В (15; 20; 25) построить эпюр и указать ее положение в пространстве.	I II III IV

3. Построить точку С', симметричную точке С относительно фронтальной плоскости проекций. Указать, в какой четверти пространства находится точка С'.

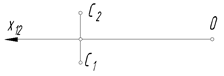
I II III IV

Пример 1. Какими координатами определяется горизонтальная проекция точки А? Указать на эпюре (чертеже)

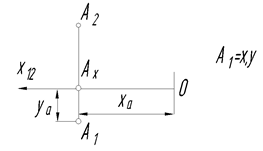
Рис. 21

Пример 2. По чертежу определить координаты точки В и ее положение в пространстве

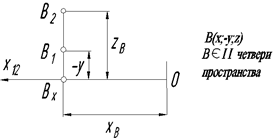
Рис. 22

Пример 3. Построить недостающую проекцию точки С (С₂), если она принадлежит плоскости проекций и определить ее положение в пространстве.

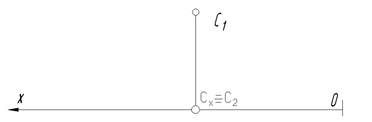
Рис. 23

Точка принадлежит плоскости проекций, если одна из координат будет равна «0», так как на чертеже задана горизонтальная проекция точки С₁, которая определяется координатами Х и Y, то значение Z должно быть равно «0». Поэтому на эпюре С_х º С₂. Так как значение Y отрицательное, то С Î задней поле П₁.

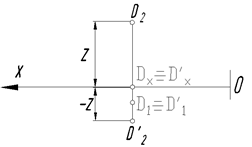Пример 4. Построить точку D^¢, симметричную точке D относительно горизонтальной плоскости П₁.

Исходная точка D располагается в I четверти пространства, симметричная точка D¢ переместится в IVчетверть. При переходе точки из I четверти в IV-ю изменится только направление координаты Z, координаты Х и Y останутся неизменными, поэтому D₁ º D¢₂.

Рис. 24

Рис. 24  

Контрольные вопросы

1. Основные способы проецирования.

2. Свойства параллельного проецирования.

3. Что такое эпюр Монжа?

4. Что такое четверти пространства?

5. Как образуются проекции А₁, А₂,А₃ точки А?

6. Какими координатами определяются:

- горизонтальная проекция точки;

- фронтальная проекция точки;

- профильная проекция точки?

7. В каких случаях на эпюре (чертеже) горизонтальная и фронтальная проекции точки совпадают?

8. Что называется биссектрисой плоскостью и каковы ее свойства?

9. Как по чертежу определить расстояние от точки до плоскости П₁,П₂,П₃?

Дата добавления: 2013-12-13