Взаимное положение прямых

Деление отрезка прямой в заданном отношении.

Прямые, перпендикулярные плоскостям проекций.

Прямые частного положения, перпендикулярные какой-либо плоскости проекций, называются проецирующими прямыми.

На рис. 30 приведены чертежи прямых:

АВ ^ П₁ – горизонтально-проецирующая прямая; А₂В₂ = ç АВ ç; a = 90⁰; b = 0;

СD ^ П₂ – профильно-проецирующая прямая; С₁D₁ = ç CD ç; a = 0; b = 90⁰;

EF ^ П₃ – профильно-проецирующая прямая; E₁F ₁ = E₂F₂ = ç EF ç; a = 0; b = 0; g = 90⁰;

g - угол наклона прямой EF к плоскости проекций П₃.

Проекции точки К, принадлежащей прямой АВ, должны принадлежать соответствующим проекциям этой прямой, т.е.

К Î АВ Þ К₁ Î А₁В₁, К₂ Î А₂В₂.

Чтобы разделить на чертеже отрезок прямой в заданном отношении, надо разделить в этом же отношении его проекцию (см. свойства параллельного проецирования).

На рис. 31 точка К делит отрезок АВ в отношении 2:3.

Две прямые в пространстве могут пересекаться, скрещиваться и быть параллельными.

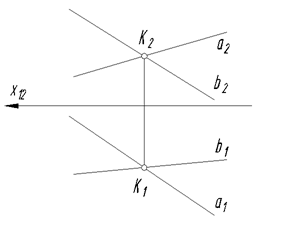
1. Пересекающиеся прямые – прямые, имеющие одну общую точку.

₀

Если прямые пересекаются, то на эпюре пересекаются и их одноименные проекции, а проекции точки пересечения К лежат на одной линии связи, т.е.

К = а Ⴖ b Þ а₁ Ⴖ b₁; К₂ = а₂ Ⴖ b₂.

2. Параллельные прямые – прямые, пересекающиеся в несобственной точке (т.е. прямые, которые лежат в одной плоскости и пересекаются в бесконечно удаленной точке).

Если прямые параллельны, то параллельны и их одноименные проекции на все три плоскости проекций. Для того, чтобы сделать вывод о параллельности прямых общего положения, достаточно параллельности их одной проекций на две плоскости проекций, т.е.

а ‖ b Þ а₁ ‖ b₁; а₂ ‖ b₂.

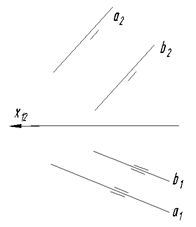
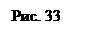
Для прямых частного положения необходимо, чтобы были параллельны их проекции на той плоскости проекций, которой эти прямые параллельны.

3. Скрещивающие прямые – прямые, не имеющие ни одной общей точки.

На эпюре (рис. 34) точки пересечения проекций этих прямых не лежит на одной линии связи, перпендикулярной к оси Х. На чертеже скрещивающихся прямых c и d точки 1, 2 и 3, 4 называются конкурирующими.

На горизонтальной проекции будет видимой та из конкурирующих точек 3 и 4, которая расположена выше относительно П₁ (Z₄ > Z₃), т.е. точка 4; на фронтальной проекции видимой будет точка 2, т.к. она расположена ближе к наблюдателю (Y₂>Y₁).

Дата добавления: 2013-12-13