Пересечение плоскостей

Линией пересечения двух плоскостей является прямая. Следовательно, в общем случае для построения линии пересечения двух плоскостей необходимо найти две точки, каждая из которых принадлежит обеим плоскостям, эти точки и определяют линию пересечения плоскостей.

Рассмотрим сначала частный случай пересечения плоскостей, когда одна из пересекающихся плоскостей занимает частное положение (параллельна плоскости проекций).

		б)
	а)

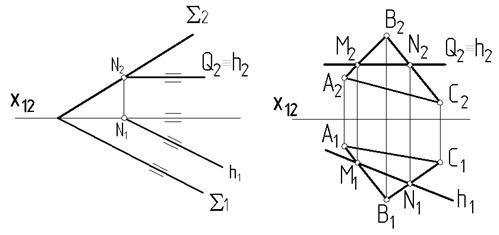
Рис. 65

На рис. 65 показано пересечение заданных плоскостей с плоскостью Q (Q ‖ П₁). В этом случае линия пересечения, принадлежащая плоскости Q, будет также параллельна плоскости П₁, т.е. будет являться горизонталью (h) пересекающихся плоскостей. Если одна из пересекающихся плоскостей (Q) параллельна фронтальной плоскости проекций П₂ (рис. 66), то линией пере-

сечения двух плоскостей будет являться прямая, параллельная плоскости П₂, т.е. будет являться фронталью ¦.

º

º

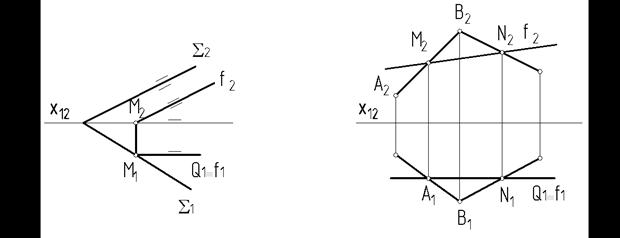Рис. 66

Рассмотрим случай пересечения двух плоскостей общего положения. Задачу на построение линии пересечения плоскостей можно решить двумя способами.

1 способ: Построить точки пересечения двух прямых одной плоскости с другой плоскостью, т.е. два раза использовать схему решения задачи на пересечение прямой с плоскостью (данный способ будет рассмотрен ниже)

2 способ: Провести две вспомогательные секущие плоскости G и ∆ частного положения. Построить их линии пересечения с заданными плоскостями. Две полученные точки пересечения Р и М этих линий определяют искомую линию пересечения данных плоскостей (рис. 67).

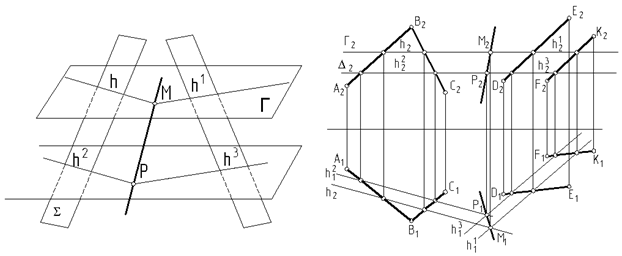
Рис. 67 Рис. 68

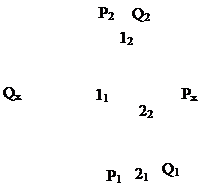
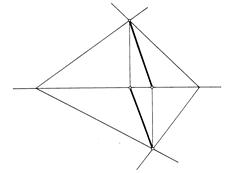Строим линию пересечения двух плоскостей: S (АВ Ⴖ ВС) и q (DE ‖ FK) (рис. 68). Для нахождения точек Р и М этой линиипересечения рассечем заданные плоскости S и q двумя вспомогательными горизонтальными плоскостями уровня Г (Г₂) и ∆ (∆₂). Из чертежа видно, что плоскость Г (Г₂) пересекается с каждой из заданных плоскостей по горизонталям h (h₁,h₂) и h¹ (h¹₁, h¹₂), которые пересекаются в точке М (М₁, М₂). Плоскость ∆ (∆₂) пересекается с заданными плоскостями по горизонталям h² (h²₁, h²₂) и h³ (h³₁, h³₂), которые пересекаются в точке Р (Р₁, Р₂). Полученные точки Р и М находятся во вспомогательных секущих плоскостях уровня Г и ∆, принадлежат также двум заданным плоскостям S и q, а значит и определяют линию пересечения МР (М₁Р₁, М₂Р₂) данных плоскостей. Рис. 69

Рассмотрим на примере построение линии пересечения двух плоскостей, заданных следами.

Если пересекаются две плоскости, заданные следами, то общими точками, определяющими линию взаимного пересечения, являются точки пересечения их одноименных следов: 12 = Р Ⴖ Q, (рис. 69).

Дата добавления: 2013-12-13