Способ замены плоскостей проекций

Способ замены плоскостей проекций заключается в выборе новой дополнительной плоскости проекций, выбранной определенным образом. При этом геометрический объект не изменяет своего положения в пространстве. При выборе новой плоскости проекций должен соблюдаться основной принцип ортогонального проецирования (метод Монжа) - плоскости проекций должны быть взаимно перпендикулярны, т.е. новую плоскость проекций необходимо располагать перпендикулярно одной из исходных плоскостей проекций П₁, П₂, П₃. Все свойства геометрического образа, отнесенные к основной системе плоскостей проекций, справедливы и для дополнительной системы плоскостей проекций.

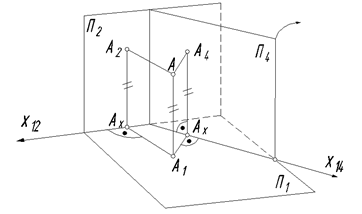
На рис. 80 показан принцип замены плоскостей проекций П₁ и П₂ и точка А в этой системе. Спроецируем точку А на плоскости П₁ и П₂ и получим ее проекции А₁ и А₂. Новая фронтальная плоскость проекций П₄ расположена перпендикулярно горизонтальной плоскости проекций П₁. Спроецируем точку А на эту плоскость, обозначив полученную проекцию А₄. Горизонтальная плоскость проекций является общей для двух систем плоскостей проекций: П₁/П₂ и П₁/П₄. Переход от одной плоскости проекций к другой будем записывать следующим образом: П₁/П₂ → П₁/П₄ и т.д.

		Рис. 81
	Рис. 80

При переходе от одной системы плоскостей проекций к другой (П₁/П₂ → П₁/П₄) видим, что аппликата Z точки А и ее горизонтальная проекция А₁ остаются неизменными, постоянными (инвариантными).

Переход от одной системы плоскостей проекций к другой легко проследить и на ортогональном чертеже (рис. 81). На чертеже мы имеем плоскости проекций П₁ и П₂, ось проекций Х₁₂, проекции точки А (А₁,А₂), точку А_х (пересечение линии связи с осью Х₁₂). Проводим новую ось проекций Х₁₄, которая определяет положение новой плоскости проекций П₄ и строим новую точку А _х¢, опуская перпендикуляр из точки А₁ на новую ось Х₁₄. Отложим на нем отрезок А_хА₄ = А_хА₂ = Z. Новая фронтальная плоскость проекций П₄ является горизонтально проецирующей плоскостью для системы П₁/П₂. Аналогично можно заменить горизонтальную плоскость проекций П₁ на новую плоскость (П₅), которая для новой системы П₁/П₄ будет фронтально-проецирующей плоскостью.

Замена одной из плоскостей проекций не всегда может решить поставленную задачу. Иногда приходится менять две и более плоскостей проекций. Построения, выполняемые в процессе последовательной замены двух плоскостей проекций, принципиально ничем не отличается от построений, производимых при замене одной плоскости проекций. При этом необходимо учитывать, что расстояния новых проекций точек от новой оси равны расстояниям заменяемых проекций от предыдущих осей (рис. 82).

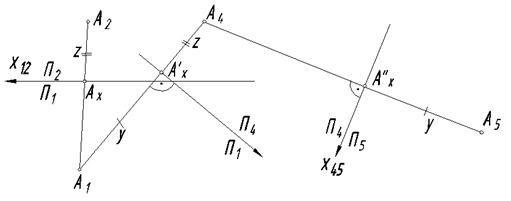
Рис. 82

Переход от одной системы к другой запишем как: П₁/П₂ → П₁/П₄ → П₄/П₅. проекция точки А на плоскость П₄ построена известным способом (см. рис. 81). Для построения проекции А₅ на плоскость П₅ из точки А₄ опущен перпендикуляр на новую ось проекций Х₄₅ и на этом перпендикуляре отложен отрезок А_х ² А₅ = А_х ¢ А₁ = Y.

Дата добавления: 2013-12-13