СВ непрерывного типа. Плотность распределения вероятностей

СВ непрерывного типа – такая СВ, которая в результате опыта может принимать любые значения из данного интервала.

Для такой СВ нельзя казать все значения, их кол-во бесконечно!, а вероятность любого конкретного значения = 0! Следовательно говорить о распределении вероятностей между отдельными значениями не имеет смысла. Как быть? Как и для геометрической вероятности введем понятие вероятного попадания случайной величины на конкретный интервал или вероятность того, что СВ примет значение из некоторого интервала Р(а < X < b), где a и b – границы интервала.

Но для случайного события геометрическая вероятность определялась для условий, когда вероятность попадания случайной точки на участок l зависела лишь от размеров этого участка и не зависела того, где находится участок на отрезке L, определяющего область возможных попаданий случайной точки, т.е. из условия равновозможности исходов!

Для СВ непрерывного типа такое условие является частным ограничением, а в общем случае вероятность попадания случайной точки на некоторый интервал зависит как от величины этого интервала, так и от его положения в области возможных значений СВ. Следовательно, чтобы задать закон распределения для СВ непрерывного типа необходимо указать область возможных значений этой СВ и правило, определяющее соответствие между любым интервалом в области значений СВ и вероятностью того, что СВ в результате опыта примет значение из этого интервала.

Для получения такого правила введем понятие «Плотности вероятности». (Аналогия из физики: плотность вещества = массе, приходящейся на единицу объема. Для неоднородного вещества – ‘местная плотность’, т.е. в точке; также в ТВ мы будем рассматривать ‘местную’ плотность вероятности - вероятность, приходящаяся на единицу длины в данной точке Х).

Плотность вероятности непрерывной СВ Х называется предел отношения вероятности попадания СВ Х на малый участок, примыкающий к т. x, к длине этого участка, когда последняя стремиться к 0.

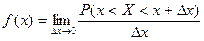
К понятию «плотности вероятности» легко перейти от родственного ему понятия «плотность относительной частоты». Например, СВ Х – рост человека, измеряемый для всех, кто проходит мимо аудитории в течении лекции. Пусть это будет 100 измерений = n’. Все значения принадлежат интервалу 150-200 см. Разобьем его на участки по 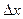= 5см и посчитаем сколько значений попадает в каждый участок., т.е. частоту попадания m_I^’. Перейдем к относительной частоте P_i‘= m_i'/n', а затем к плотности относительной частоты f_i = P_i’/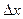. Для наглядности представим это на графике, называемом гистограммой:

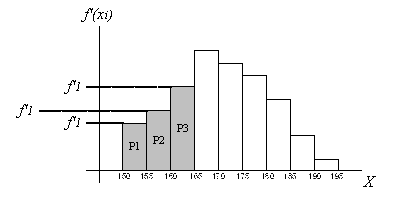
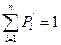
Высота столбца – плотность относительной частоты соответствующего участка. Площадь столбца – относительная частота.

Пр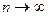и и 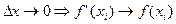, с тупенчатая фигура (гистограмма) распределения относительной частоты сглаживается в кривую, называемую кривой распределения вероятностей, а соответствующая ей функция f(x) – функция плотности вероятности или закон распределения. Кривая распределения обладает следующими свойствами:

- ордината кривой распределения в т.Х численно равна плотности вероятности в т.Х.

- площадь, ограниченная кривой распределения на интервале (а, b) численно равна вероятности попадания СВ в этот интервал

- площадь, ограниченная кривой распределения на всем интервале возможных значений СВ X, численно равна 1.

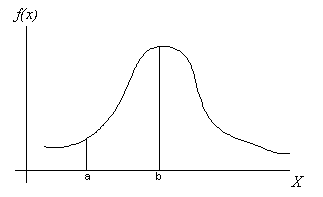
Свойства функции плотности распределения вероятностей:

1)

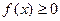
2)

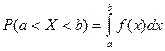
3) 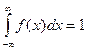- Это свойство часто называют нормировочным условием функции плотности распределения вероятностей.

Т.о., мы ввели понятие закона распределения для СВ непрерывного типа в виде функции плотности распределения вероятностей или ее графического представления в виде кривой распределения.

В ТВ для СВ непрерывного типа рассматривается достаточно ограниченное число типовых законов распределения, основные из которых мы рассмотрим позднее.

Дата добавления: 2013-12-14