Свойства МО

МО непрерывной СВ

МО непрерывной СВ называют определенный интеграл от произведения СВ на свою функцию плотности распределения вероятностей, взятый по всей области возможных значений СВ.

Пример 3:

СВ X распределена равномерно на отрезке (a,b). Определить M(X).

1.

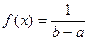
2.

Вероятностный смысл МО: При многократном наблюдении одной и той же СВ в неизменных условиях ее наблюдаемое среднее значение “по вероятности” стремиться к МО.

Механический смысл МО: абсцисса центра тяжести распределения “масс” вероятности

Физический смысл: «истинное» значение многократно измеряемой величины

Свойство 1.

Свойство 2.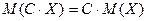

Свойство 3.

Свойство 4.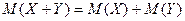

X	x1	x2	+	Y	y1	y2
P	p1	p2	P	g1	g2

X+Y	x1+ y1	x1+ y2	x2+ y1	x2+ y2
P	p1g 1	p1g 2	p2g 1	p2g2

Следствие:

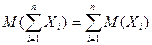
Свойство 5. МО произведения 2-х независимых* СВ равно произведению их МО:

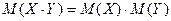
X	x1	x2	+	Y	y1	y2
P	p1	p2	P	g1	g2

X+Y	x1y1	x1y2	x2y1	x2y2
P	p1g 1	p1g 2	p2g 1	p2g2

Следствие: МО произведения n независимых СВ равно произведению их МО

(*) Примечание: Две СВ называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая СВ. Несколько СВ называются взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.

А теперь вернемся к Примеру 2б, и покажем используя 4-е свойство МО правильность ответа (M(X)=np). Действительно, СВ X можно представить как сумму СВ X_i, каждая из которых характеризует соответствующее число появлений события A в каждом опыте, имеющие одно и тоже МО, равное p (Пример 2а). Тогда:

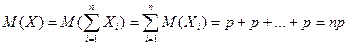
Замечание 1. Если M(X) существует, X-непрерывная СВ и ее функция плотности f(x) является четной функцией, то M(X)=0

Замечание 2. Если M(X) существует, и если f(x) симметрична относительно некоторой точки x = a, то M(X) = a. МО СВ X есть центр симметрии.

Замечание 3. МО СВ X имеет ту же размерность, что и СВ, а значение M(X) не всегда совпадает с одним из возможных значений СВ, но всегда лежит в интервале (x_min, x_max)

Дата добавления: 2013-12-14