Лекция 13. Расчет продолжительности инсоляции

Проецирование на дополнительную плоскость.

Применяется для построения истинного вида фигуры или линии. Для этого вводится плоскость, параллельная фигуре или линии, и строится ее проекция на эту плоскость. Эта проекция является истинным видом фигуры.

Объяснить суть замены плоскостей проекций и проецирования на дополнительную плоскость. Для этого загрузить файл mong_3 из лекции 2 и utility_3c.lsp. Показать в динамике разворот плоскостей при построении чертежа.

Решить задачи 1.9, 1.11.

Привести пример по 3d, эквивалентный проецированию на дополнительную плоскость:

1. Построить параллелепипед;
2. задать ПСК как некоторую секущую плоскость;
3. построить сечение этой плоскостью (section);
4. создать дополнительное видовое окно;
5. скопировать ПСК дополнительной плоскости из старого окна в новое (ucs / apply);
6. в новом окне выполнить команду plan.
7. построить вид в плане ПСК (команда plan).

Инсоляция

– освещение комнат и территорий прямыми солнечными лучами. Инсоляция оказывает благоприятное и необходимое для жизнедеятельности биологическое воздействие. Поэтому обеспечение И. является обязательной частью архитектурно-строительного проектирования.

Нормы инсоляции

Нормируется продолжительность И. Инсоляция нормируется и рассчитывается на день равноденствия: 22 марта или 22 сентября. Может понадобиться продолжительност инсоляция и на любой другой день, например на день летнего солнцестояния 22 июня.

Инсоляция может быть непрерывной и прерывной.

Условия расчета:

1. Продолжительность непрерывной инсоляции в комнате должна быть не менее 2 часов.
2. Продолжительность прерывной инсоляции – не менее 2.5 часа.
3. Не учитывается 1 час от восхода и 1 час перед закатом солнца.
4. Не учитываются по 8 градусов в обе стороны от стены, на которой расположено окно.
5. При прерывистой инсоляции хотя бы один интервал света должен быть более 1 часа.
6. При расчете2-х комнатной квартиры должна быть необходимая инсоляция хотя бы в одной комнате, для 3-х комнатной – в двух комнатах.

Геометрическая модель расчета инсоляции

Из астрономии:

Солнце движется по небосводу относительно расчетной точки по окружности.

В день равноденствия плоскость движения – вращения солнца (плоскость равноденствия) проходит через расчетную точку (точка окна квартиры). Угол j наклона плоскости отсчитывается от нормали к земле и равен широте местности. Для Челябинска j=55° (соотвтественно, угол между плоскостью равноденствия и горизнотальной плоскостью является дополнительным и равен для Челябинска 35°.

В неравноденствие плоскость вращения смещается параллельно плоскости равноденствия летом вверх, зимой вниз. Пучок солнечных лучей представляет собой конус вращения с вершиной в расчетной точке. Угол конуса d отсчитывается от плоскости равноденствия по формуле ,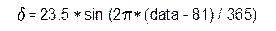

где data – день расчета, отсчитываемый от 1 января. Например, 22 марта – 81 день. Отсюда для равноденствия d=0. Максимальный угол конуса d= 23.5° приходится на 22 июня – 173 день.

Световые потоки ограничены сечениями зданий лучевой плоскостью (в равноденствие) или лучевым конусом (в неравноденствие).

Показать файл: Траектории солнца_1.dwg.

Показать кадры анимации суточного движения тени.

Продолжительность инсоляции определяется по сумме углов света, измеренных в плоскости равноденствия. Перевод углов в часы: 1 час = 360:24 =15°. 1° = 60 мин:15= 4 мин. Шкала времени – астрономическая (в 12 час. дня солнце на юге). При необходимости производят переход на местное время. Продолжительность инсоляции не зависит от шкалы времени, поскольку определяется разностями значений времени.

Порядок расчета на день равноденствия:

Для 3d модели:

1. Построить модели зданий как solid-объекты. Поставить маркер точки в расчетную точку окна.
2. Задать плоскость равноденствия как ПСК:
• перейти в окно аксонометрии;
• задать МСК;
• перенести начало координат в расчетную точку – ось X направлена на восток, ось Y – на север;
• повернуть ПСК вокруг оси Z на 180° – ось X направлена запад, ось Y – на юг.
• Повернуть ПСК вокруг оси X на угол (j – 90). Для Челябинска на +35°.
3. Построить сечения (section) зданий плоскостью ПСК.
4. Скопировать окно аксонометрии и установить в нем вид в плане ПСК (_plan / current). Убедиться, что ось Y направлена верх (на юг), ось X – вправо (на запад).
5. В плоскости равноденствия проставить угловые размеры световых углов. Через расчетную точку провести отрезок с востока на запад. Определить сумму световых углов. Вычесть ограничения на восходе и закате, если они видны из окна. Если луч света скользит вдоль стены, вычесть от каждой стены по 8°. Перевести градусы в часы и минуты. Сделать вывод о соблюдении норм инсоляции в расчетной точке окна.

Показать3d-модель задачи из тетради.

Для 2d-модели (расчет методами начертательной геометрии)

1. Построить вид слева. Обозначить проекции расчетной точки.
2. Задать плоскость равноденствия как профильно-проецирующую под углом 35° от земли.
3. Ввести дополнительную плоскость П₅, параллельную плоскости равноденствия с осью X₃₅.
4. Строить проекции линии пересечения зданий с плоскостью равноденствия на дополнительную плоскость П₅. Нанести проекцию расчетной точки
5. На П₅ через проекцию расчетной точки окна провести отрезок восход-закат, перпендикулярно оси X₃₅.
6. Измерить световые углы….

Решить задачу в тетради

3d-модель расчета на 22 июня

1. Повторить построение моделей и плоскости равноденствия. Сохранить ПСК или копию видового окна с этой ПСК.
2. Повернуть плоскость равноденствия вокруг оси X на 90°.
3. Построить контур конуса света с углом d от оси Х равным 23.5°. Объединить линии контура и вращать вокруг оси Y.
4. Создать оболочку с конической поверхности. Толщина оболочки 0.001.
5. Командой interfere (Взаимод) построить сегменты сечений конической оболочки с моделями зданий.
6. Определить луч восхода и заката солнца. Для этого установить горизонтальную ПСК в расчетную точку – вершину конуса – это плоскость горизонта. Командой slice (Разрез) удалить части конуса ниже плоскости горизонта. Образующие среза являются лучами восхода-заката.
7. Восстановить ПСК равноденствия, вид в плане на эту ПСК. Ставить в этой плоскости угловые размеры секторов света…

Построить 3d-модель той же задачи на 22 июня.

Показать файл задания и чертеж с его решением по НГ.

Дата добавления: 2013-12-14