N с параметрическими отказами

N циклического функционирования (реле, электроклапаны и т.д.)

N непрерывного функционирования

N одноразового (пиропатроны и т.д.)

Тема 2. Общие вопросы и понятия в надежности сложных технических объектов в АТ.

Структурная схема надежности отображает деление системы на элементы и влияние отказов элементов на надежность системы без учета в явном виде физических процессов функционирования системы.

Модель функционирования - это математическое описание физических процессов функционирования системы в условиях случайных возмущений.

Структурно-функциониальная схема надежности - комбинация структурной схемы надежности и модели функционирования.

Количественные характеристики надежности

По характеру функционирования различают четыре вида элементов:

Надежность элементов одноразового срабатывания характеризуется вероятностью Р безотказного срабатывания, статистическую оценку которой определяют по результатам испытаний

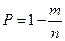
где n -число элементов, взятых для испытаний,

m - число отказавших элементов.

Надежность невосстанавливаемого элемента, где Т - время от включения элемента до его отказа (время безотказной работы) случайно и при заданной наработке t определяются следующие характеристики надежности:

- вероятность безотказной работы (ВБР) (функция надежности)

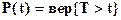
- вероятность отказа (функция ненадежности)

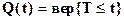
- плотность вероятности отказа

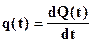
- интенсивность отказов (условная плотность вероятности отказа)

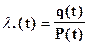
среднее время безотказной работы (математическое ожидание времени безотказной работы)

Т_ср = M [T]

поскольку безотказное состояние и отказ образуют полную группу событий, то

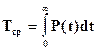
преобразуя вышеуказанные уравнения получаем Зависимость между вероятностью безотказной работы и интенсивностью отказов

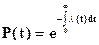
Существуют три характерных периода работы элементов:

n приработки, в течении которого интенсивность отказов снижается по мере «выжигания» наиболее «слабых» элементов

n нормальной работы с постоянной интенсивностью отказов

n старения и повышенного износа, сопровождающегося нарастанием интенсивности отказов

для нормальной работы справедлив экспоненциальный закон распределения времени безотказной работы, т.е. при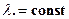

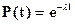- это основная расчетная зависимость для случая внезапных отказов. Статистические данные по эксплуатации позволяют оценить интенсивность типовых комплектующих элементов применяемых в авиастроении. Отличие реальных условий от обобщенно номинальных учитывается поправочным коэффициентом k_s по зависимости

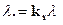
Количественные характеристики надежности невосстанавливаемых элементов циклического функционирования аналогичны рассмотренным. Различие состоит в замене случайного времени Т случайным числом циклов R от момента включения до отказа и выражении наработки заданным числом циклов r срабатывания за время функционирования.

Например ВБР невосстанавливаемых элементов циклического функционирования равно

Р= вер {R>r}

Процесс эксплуатации восстанавливаемого элемента непрерывного функционирования представляет собой последовательность случайных по продолжительности интервалов времени Т_i безотказной работы и чередующихся вместе с ними случайных интервалов t_i простоя, во время которого происходит его восстановление.

Иногда Т_i, а величину - суммарной наработкой на отказ

Коэффициент готовности вероятность K(t) того, что в произвольный момент времени элемент находится в работоспособном состоянии. Вероятность K(t) равна сумме вероятностей безотказной работы элемента на интервале [0,t] и вероятности того, что элемент, отказавший в этом интервале, был восстановлен к концу этого интервала. Под коэффициентом готовности, в надежности, принимают то стационарное значение, к которому стремится функция K(t) с ростом времени

Кг = lim K(t)

Можно показать, что для любых распределений времени Т_i (t) и t_i (t) пределом вероятности K(t) является отношение средних значений

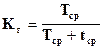
Варианты структурной схемы надежности

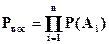
Последовательное соединение

Параллельное соединение

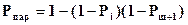
Смешанная схема.

Дата добавления: 2013-12-14