Инженерные методы определения вероятностных характеристик параметров состояния

Числовые характеристики параметров состояния(математические ожидания, дисперсии и т.д.), необходимые для расчета параметрической надежности, на этапе проектирования ЛА чаще всего неизвестны. Возникает задача нахождения числовых характеристик распределения параметров состояния по известным числовым характеристикам возмущающих параметров, обуславливающих стохастический характер функционирования рассматриваемого объекта.

Решение этой задачи базируется на математической модели процесса функционирования объекта как динамической системы. За основу принимается детерминированная модель функционирования, используемая при проектировании объекта. Модель отображает преобразования случайных входных параметров (возмущений) в выходные параметры динамической системы(параметры состояния).Универсальным методом нахождения закона распределения f(z)параметра состояния по известным законам F_i(x_i) возмущений, пригодным практически для любых математических моделей, является метод статистического моделирования (метод статистических испытаний, или метод Монте-Карло).

Сущность метода заключается в том, что зависимость параметра состояния от возмущений реализуется многократно, всякий раз при новых случайных значениях X_i. Полученные случайные значения параметра состояния подвергаются статистической обработке подобно результатам натурных испытаний объекта. Каждая операция задания путем случайного выбора значений возмущающих параметров называется пробой.

Статистическое моделирование основывается на формировании последовательности случайных чисел, подчиняющихся заданному закону распределения, причем исходным является

Надежность конструкции ЛА

Постановка задачи расчета надежности элементов конструкции.

Элементами конструкции ЛА называют силовые элементы (отсеки фюзеляжа, крылья самолетов, рамы крепления двигателей и приборов, отдельные детали силового набора - шпангоуты лонжероны и т.д.)

Отказ элемента конструкции -это достижение предельного состояния, т.е. исчерпание несущей способности соответственно по прочности, устойчивости и т.д.

Вероятность безотказной работы элемента конструкции -это вероятность неразрушения т.е. вероятность того, что в течении заданного времени в определенных условиях эксплуатации не наступит ни одно из возможных предельных состояний.

Многообразие процессов приближения состояния конструкции к отказу можно привести к двум схемам: к мгновенному разрушению и к накоплению повреждений.

По схеме мгновенного разрушения под предельным состоянием понимают такое состояние, при котором действующая на элемент нагрузка S становится равной разрушающей нагрузке R, соответствующей исчерпанию несущей способности. Часто, нагрузку R называют несущей способностью. Область безотказных состояний определяется условием S<R, область отказов условием 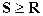. В качестве нагрузки и несущей способности должны быть выбраны одни и те же физические параметры.

Например, в строительной механике широко используют сопоставление эквивалентного напряжения 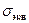с допустимым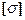 , т.е. проверяя, что

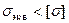
По схеме накопления повреждений в качестве параметра состояния принимают суммарное относительное повреждение

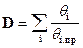
где 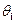- мера повреждения, накопленных повреждений конструкцией на i -ом этапе эксплуатации,

а 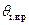- предельная мера повреждений в условиях i -ого этапа.

За меру повреждений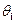можно принимать деформацию, полученную на i -ом этапе, число циклов нагружения, если возможно усталостное разрушение, либо действие нагрузки i-ого типа. Предельным значением 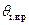является соответственно допустимая деформация, число циклов i -ого типа (с i -ой амплитудой и частотой), доводящее конструкцию до разрушения, либо время, необходимое для разрушения конструкции под действием нагрузки i -ого типа.

Большинство случайных возмущающих факторов изменяются во времени. Поэтому и нагрузки и несущая способность конструкции в общем случае - случайные функции времени, а нередко и координат.

Прямой путь решения этих задач осложнен отсутствием, как правило, информации о законах распределения, что приводит исследователей к необходимости зачастую решения обратной задачи - оценки времени наступления отказа в слабом звене и при котором нагружение особенно опасно.

В общем случае полагают, что существует n предельных состояний конструкции, на практике обычно ограничиваются рассмотрением одного-двух. Возможные предельные состояния в общем случае зависимы. Однако, неучет корреляционных связей при достаточно высокой надежности конструкции вносит незначительную погрешность, вполне допустимую в расчетах первого приближения.

Напряженно-деформированное состояние отдельных элементов конструкции различно ввиду особенностей формы, силовой схемы и условий нагружения. Поэтому надежность их следует определять в отдельности, объединяя затем результаты в ССН с учетом того, что отказы элементов могут быть зависимыми в силу общих нагрузок и взаимосвязи элементов в общей силовой схеме ЛА. Элементы конструкции ЛА, за редким исключением, не резервируются, а следовательно ССН конструкции имеет вид последовательного соединения.

Дата добавления: 2013-12-14