Внутренние силовые факторы и напряжения при изгибе

При плоском поперечном изгибе в случае отсутствия осевых нагрузок в поперечных сечениях балки возникают два внутренних силовых фактора: изгибающий момент М _x и поперечная сила Q _y. При расчете конструктивных элементов машин поперечная сила в сечении обычно не учитывается ввиду ее малости.

При анализе внутренних силовых факторов используют, как описано выше, метод сечений. Разбивая мысленно балку на однородные участки, составляют уравнения равновесия сил для отсеченных частей. из которых находят изгибающие моменты М _x в сечениях.

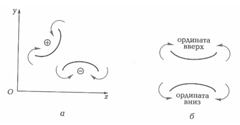Знак момента в поперечном сечении определяется по знаку кривизны изогнутой балки (рис.2.7,а). При построен эпюр моментов ординаты откладываются на сжатых волокнах (рис.2.7,б).

	Рис.2.7. Схема для определения знака изгибающего момента по знаку кривизны балки на рассматриваемом участке: момент положителен, если растянутые волокна внизу

После определения изгибающих моментов в поперечных сечениях балки могут быть исследованы внутренние напряжения.

Рассмотрим прямолинейную балку постоянного сечения (рис.2.8), к торцам которой приложены изгибающие моменты М (чистый изгиб).

	Рис.2.8. Напряжения в поперечных сечениях балки при чистом изгибе

В этом случае изгибающий момент в всех поперечных сечениях постоянный М _x = М. Под действием внешних моментов М балка изогнется, при этом все сечения останутся плоскими и нормальными к его оси, однако горизонтальные слои-волкна на выпуклой стороне удлиняются, а на вогнутой - укорачиваются. Слой, совпадающий с осью балки, не изменяет своей длины и поэтому называется нейтральным слоем.

При чистом изгибе в поперечном сечении возникают нормальные напряжения s, которые возрастают по линейному закону по мере удаления от нейтральной линии (продольной нейтральной плоскости), где s = 0. Эта линия перпендикулярна к поперечным сечениям и проходит через их центры тяжести, т.е совпадает с осью балки. Максимальные значения напряжений в точках сечения, наиболее удаленных от нейтральной оси, находятся по формуле

, (2.6)

где осевой момент сопротивления W _x поперечного сечения балки при изгибе относительно оси x (размерность м³), для сечений приводится в справочниках.

Значение W _x для основных видов сечений определяется по формулам

• для круглого сечения диаметром d: W _x = 0,1d³; (2.7)
• для прямоугольного сечения шириной b и высотой h: W _x = bh ²/6 (2.8)

Построение эпюр изгибающих моментов в опасных сечениях

Работа выполняется в такой последовательности: 1) определяются реакции опор; 2) выявляются все внутренние силовые факторы в сечениях на отдельных участках балки; 3) выполняется построение эпюр моментов.

Рассмотрим построение эпюр для балки, показанной на рис.2.9.

	Участок 1		Участок 2

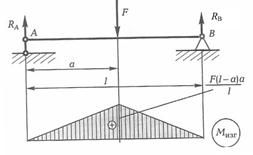
Рис.2.9. Однопролетная балка, нагруженная

поперечной силой и ее эпюра изгибающих

моментов в поперечных сечениях

1. Реакции опор из уравнений моментов относительно шарниров А и В составляют

S M_А = 0: R _B = Fa/l и S M_В = 0: R _A = F(1- a) /l.

2. Разбиваем балку на два участка: 1 - от опоры А до силы F, 2 - от опоры В до F.

Для определения величин внутренних изгибающих моментов М_х на первом и втором участках запишем уравнения моментов в сечениях на расстоянии z ₁ и z ₂:

1-й участок при момент М_х1 = R _A∙ z₁ = F (1- a)z₁ /l; M_{x max} = F (1- a) a/l при z₁ = а.

2-й участок при момент М_х2 = R _A∙ z₂ - F (z ₂ - a); M _{x max} = F (1- a) a/l при z₂ = а.

На опорах при z₁ = 0 и z₂ = l изгибающий момент _max = M _{x min} = 0.

3. Строим эпюру изгибающих моментов.

Проводим горизонтальную ось под схемой балки и на вертикалях, проходящих через опоры А и В, а также по линии действия силы F откладываем соответствующие значения момента M _x. Значение M _{x max} откладываем вверх (на сжатых волокнах), - величина положительная. Соединяем эти значения прямыми линиями, поскольку зависимость M _x от координаы сечения z линейная.

Дата добавления: 2013-12-14