Напряжения и деформации при сдвиге (срезе)

Сдвиг и кручение

Кроме деформаций растяжения. сжатия или изгиба материал может испытывать деформацию сдвига. Как показано в разделе 2.1 (см. таблицу 2.1), при воздействии внешних нагрузок в поперечных сечениях бруса возникают поперечные силы Q_x и Q_y.

Считается, что деформация сдвига (среза) возникает при действии двух равных противонаправленных сил, лежащих в плоскостях соседних поперечных сечений бруса. Параллельные сечения сдвигаются друг относительно друга на угол g с осью. При этом касательные напряжения в плоскости поперечного сечения равномерно распределены по его поверхности площадью А, так что равны

, (2.9)

где Q = F - внутренняя поперечные сила, равная соответствующей внешняя поперечной нагрузка F.

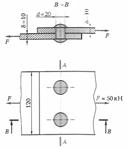На рис.2.10 показано, что под действием горизонтальных сил F может произойти срез заклепок по плоскости нахлестки соединяемых листов, так что площадь поверхности среза заклепки равна площади поперечного сечения ее стержня .

	Рис.2.10. Заклепочное соединение под действием горизонтальной нагрузки F.

Установлено, что касательные напряжения t пропорциональны угловой деформации g - это уравнение выражает закон Гука для сдвига

, (2.10)

где G - модуль упругости материала при сдвиге (имеет размерность Па или МПа); g - относительный сдвиг (величина безразмерная);

, (2.11)

Е – модуль продольной упругости материала; μ» 0,3 – коэффициент Пуассона.

Для стали G = 0,8 ×10⁵ Мпа.

Напряжения и деформации при кручении

Кручением называется такой вид деформации, при котором в поперечных сечениях бруса возникает только крутящий момент.

Рис.2.11. Круглый брус под действием крутящего момента М _кр  

М_кр

Рассмотрим кручение круглого прямого бруса (рис.2.11), жестко заделанного в стенку, к свободному концу которого приложен крутящий момент М _кр. Под действием крутящего момента смежные поперечные сечения поворачиваются друг относительно друга вокруг оси бруса, так что образующая ОВ его цилиндрической поверхности искривится и займет положение ОС.

При кручении принято считать, что ось бруса не деформируется и плоские поперечные сечения остаются такими же плоскими, а продольные волокна не меняют своей длины. Крутящий момент считается положительным, если при взгляде с торца он вращает брус против часовой стрелки. как показано на рис.2.11.

В поперечных сечениях бруса при кручении возникают только касательные напряжения (чистый сдвиг).

Угол закручивания и относительный угол закручивания связаны зависимостью

, (2.12)

где l - длина бруса.

С учетом уравнений (2.10) и (2.12) для угла закручивания установлена формула

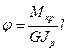, (2.13)

где J _p - полярный момент инерции сечения, для круглого бруса равный J _p = 0,1D⁴.

Касательные напряжения при кручении в сечении распределяются пропорционально расстоянию рассматриваемой точки от оси бруса - в центре они равны нулю. максимальное значение касательного напряжения находится по по формуле

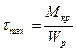, (2.14)

где W _p - полярный момент сопротивления, являющийся геометрической характеристикой поперечного сечения бруса (с размерностью м ³).

Для сплошного поперечного сечения диаметром D величина W _p = 0,2D³, а для полого вала с отверстием диаметром d равна W _p = 0,2D³(1-d⁴/D⁴). Очевидно, что валы сплошного сечения менее экономичны, чем полые, но проще в изготовлении.

Построение эпюр крутящих моментов и касательных напряжений

Эпюры крутящих моментов (внутренних силовых факторов) и касательных напряжений при кручении строятся аналогично их построению при растяжении. На схеме бруса выделяются участки с характерными величинами сечений и нагрузок, и затем выполняется анализ по участкам.

На рис.2.12 приведены результаты такого анализа для круглого бруса, с жестко закрепленным левым торцом и свободным правым. В средней части он нагружен двумя разнонаправленными крутящими моментами Т ₁ = М и Т ₂ = 2 М. С учетом перепада диаметров бруса выделено четыре расчетных участка по его длине.

Как видно из результатов анализа наибольшие значения внутренние силовые факторы и напряжения имеют место на третьем участке.

Рис.2.3. Прямой брус под действием крутящих моментов Т ₁ и Т ₂

и эпюры внутренних силовых факторов и напряжений

Дата добавления: 2013-12-14