Пища в истории человечества

План

Лекция №2 История развития физиологии питания. Основные понятия.

Следует отметить и сформулированные Н.Ф.Реймерсом (1990) с применением популярных афоризмов принципы видового обеднения (замещения) – основные закономерности, осуществляющиеся при нарушениях видового разнообразия внутри экосистем.

Волны

Образование и распространение волн в упругой среде

Если в каком-либо месте любой упругой среды (твердой, жидкой или газообразной) возбудить колебания ее частиц, то, вследствие взаимодействия между частицами, это колебание будет распространяться от частицы к частице с некоторой скоростью.

Процесс распространения колебаний в пространстве называется волной.

Частицы среды, в которой распространяется волна, не переносятся волной, а лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц, по отношению к направлению в котором распространяется волна, различают продольные и поперечные волны.

В продольной волне частицы среды колеблются вдоль направления распространения волны.

В поперечной волне частицы среды колеблются в направлениях перпендикулярных направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн.

Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые точки пространства. Геометрическое место точек, до которых доходят колебания к моменту времени 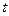, называется фронтом волны (или волновым фронтом). Другое определение: фронт волны – это граница, отделяющая колеблющиеся частицы от частиц еще не начавших колебаться.

Скорость движения каждой колеблющейся точки непрерывно меняется по величине и зависит от амплитуды, частоты и фазы колебаний. В противоположность этому, скорость перемещения фронта волны в однородной среде постоянна. Форма фронта волны определяется конфигурацией источника колебаний и свойствами среды.

Фронт волны от источника колебаний в однородной изотропной среде имеет вид сферы. Такие волны называются сферическими.

В неоднородной, анизотропной среде, а также от неточечных источников колебаний, фронт волны имеет сложную форму. Если фронт волны представляет собой плоскость и эта форма сохраняется по мере распространения колебаний в среде, то волну называют плоской.

Малые участки фронта волны сложной формы можно считать плоской волной, если рассматривать небольшие расстояния, проходимые этой волной.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесчисленное множество, в то время как волновой фронт в каждый момент времени только один.

Волновые поверхности остаются неподвижными, так как они проходят через равновесные положения частиц, колеблющихся в одинаковой фазе. Волновой фронт все время перемещается.

Волновые поверхности могут быть любой формы. В плоской волне волновые поверхности представляют собой систему параллельных друг другу плоскостей, а в сферической – систему концентрических сфер.

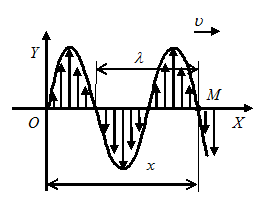Для выяснения основных характеристик волны рассмотрим простейший случай гармонического колебания, распространяющегося вдоль оси . Обозначим смещение колеблющейся точки из положения равновесия через .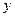

Будем считать, что источник колебаний, помещенный в точке О в момент времени 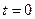совершает гармонические колебания по закону

.

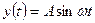Для точки М,находящейся на расстоянии 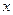от источника колебаний, начало колебаний отстает от начала колебаний точки О на промежуток времени , где - скорость распространения волны.

Обозначим смещение точки М через 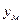, а смещение точки О – через.

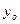В момент времени 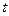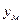будет равно смещению точки О в момент времени 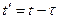, т.е.

.

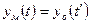Подставим вместо его выражение [].

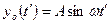Тогда

.

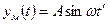Подставив в это выражение значение 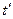, получим

.

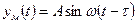С учетом того, что , выражение перепишется в виде

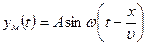. (1)

Так как 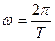, то в окончательном виде уравнение будет:

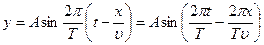- уравнение луча.

При движении волны справа налево знак скорости меняется, тогда уравнение луча запишется, как

.

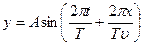Точки, в которых смещение «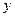» достигает своего максимального значения, называются гребнями волны, а точки, в которых «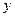» принимает минимальные значения, называются впадинами. Расстояние между двумя соседними гребнями или впадинами называется длиной волны.

Обозначается она буквой 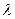. Величина 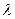есть также расстояние между двумя точками волны, фазы которых отличаются на 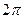. Следовательно, длина волны равна тому расстоянию, на которое распространяется волна за период:

.

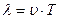С учетом этого уравнение луча может быть записано в виде:

.

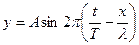Сравнивая это выражение с уравнением гармонических колебаний 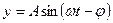, мы видим, что 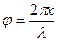- фазовый угол.

Фазовый угол 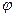показывает, насколько фаза колеблющейся точки отличается от фазы точки, находящейся в начале координат.

Групповая и фазовая скорость

Зафиксируем какое-либо постоянное значение фазы в уравнении луча, положив в уравнении (1)

.

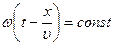Это выражение дает нам связь между временем «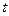» и тем местом «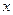», в котором зафиксированное значение фазы находится в данный момент. Определив из этого выражения 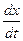, мы найдем скорость, с которой перемещается данной значение фазы.

Продифференцировав его по 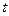, найдем

.

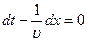Откуда .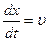

Это значит, что скорость распространения волны в уравнении луча есть скорость перемещения фазы. Поэтому ее называют фазовой скоростью.

Зависимость фазовой скорости волны в среде от частоты волны называется дисперсией. Среды, в которых наблюдается это явление, называются диспергирующими средами.

Реальные волны имеют ограниченную протяженность в пространстве и ограниченную длительность во времени. Такие волны могут быть представлены в виде совокупности или группы плоских синусоидальных волн. В диспергирующей среде происходит искажение формы этой группы волн, обусловленное различием фазовых скоростей отдельных синусоидальных волн. Для характеристики распространения группы волн и скорости переноса ими энергии понятия фазовой скорости недостаточно. Поэтому вводится дополнительное понятие – групповой скорости. Групповой скоростью называется скорость переноса энергии группой волн.

При выводе уравнения луча мы предполагали, что амплитуда колебаний с течением времени не изменяется и, что среда однородна, т.е. фазовая скорость везде одинакова. Это значит, что мы рассматривали плоскую волну, так как у сферической волны амплитуда колебаний уменьшается обратно пропорционально пройденному расстоянию. Следовательно, уравнение движения для случая сферической волны будет иметь вид

.

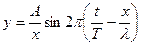Волны в сплошной среде

Колеблющиеся тела непрерывно меняют свою форму (или деформируются). В продольных волнах имеет место деформация растяжения или сжатия. При распространении поперечных волн в среде имеет место деформация сдвига. Для теоретического вычисления скорости распространения деформаций в упругой среде рассмотрим стержень, по которому ударом молотка в течение времени 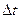сообщили некоторый импульс силы .

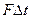За это время точки торца стержня сместились на расстояние 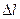, а возникшая волна сжатия пробежала участок длинной .

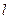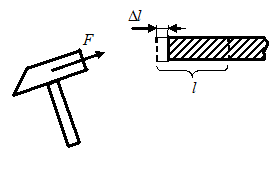Т.е.

,

где - скорость распространения волны сжатия.

Масса этого участка стержня равна

,

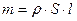где 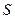- площадь поперечного сечения стержня;

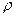- его плотность.

Импульс силы оказывает на эту часть стержня двоякое воздействие:

во-первых, он сжимает ее на длину 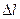, величина которой найдется из закона Гука:

,

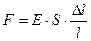где 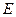- модуль упругости;

во-вторых, он сообщает этой части бруска импульс направленный вправо. Величина этого импульса, согласно закону сохранения количества движения, равна

.

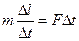Отсюда

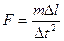
или, подставив вместо 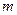ее выражение,

.

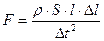Приравняв это выражение формуле силы из закона Гука, получим:

().

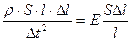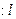Разделив на 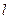, перепишем это равенство в виде

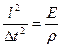
или

.

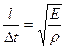Т.к. 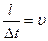, то в окончательном виде

.

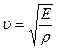Если стержень не сжимать, а растягивать, то величины 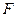и 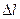изменят свой знак на обратный, а величина останется той же самой.

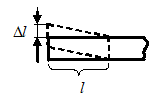В случае поперечных волн вывод формулу скорости распространения деформаций остается таким же, как и прежде, с той лишь разницей, что величины 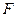и 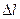будут перпендикулярны оси стержня.

Кроме того, в этом случае мы имеем другой вид деформации - деформацию сдвига. Поэтому уравнение закона Гука для сжатия следует заменить другим уравнением

,

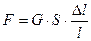где - модуль сдвига.

Скорость распространения поперечных волн получится тогда равной

.

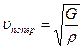В упругих твердых телах типа стержней деформации растяжения и сжатия сопровождаются небольшим изменением поперечных размеров тел. В телах больших размеров поперечные деформации затруднены и скорость распространения продольных волн равна

,

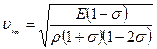где 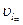- скорость распространения продольных волн в среде с большими поперечными размерами;

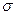- коэффициент Пуассона.

Изучая скорость распространения продольных и поперечных волн можно сделать заключение о природе веществ, через которые проходят упругие волны. На этом основаны сейсмические методы геологоразведки. При сильном взрыве через землю бегут волны деформации, скорость которых зависит от механических свойств пород. Измеряя скорость распространения волн на различных расстояниях от точки взрыва, можно оценить характер залеганий.

В жидкостях и газах деформации сдвига неупруги. Если сдвинуть один слой относительно другого, то сдвинутые слои не стремятся вернуться в исходное состояние. Поэтому в жидкостях и газах могут распространяться только продольные волны – волны расширения и сжатия.

Интерференция волн

Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Это вытекающее из опыта утверждение носит название принципа суперпозиции волн.

В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают постоянной разностью фаз, то такие волны называются когерентными. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту.

При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках – ослабляют друг друга.

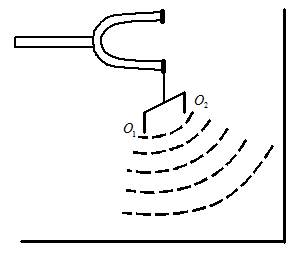
Рассмотрим простейший случай – суперпозицию когерентных волн на поверхности воды. Когерентные волны можно получить, если источники волн связаны и совершают колебания совместно, например, если волны вызываются двумя стерженьками, погруженными в воду, прикрепленными к одной из ножек камертона.

Рассмотрим чему равно результирующее колебание в какой-либо фиксированной точке 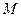. Картина рассмотрения волн от обоих источников (вид сверху) будет иметь вид:

В точке 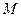уравнение колебаний вызванных первой волной будет иметь вид

.

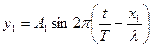То же для второй волны

.

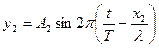Для случая, когда 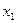не сильно отличается от 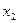, можно положить, что амплитуды обоих колебаний одинаковы, т.е.

.

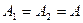Уравнение результирующих колебаний для точки 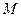запишется как

.

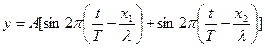Из тригонометрии нам известно, что

.

С учетом этого формула результирующих колебаний примет вид

.

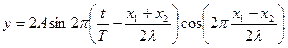Обозначим 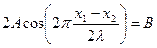. Тогда получим уравнение гармонических колебаний

.

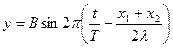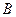- амплитуда суммарных результирующих колебаний. Величина ее зависит от разности расстояний точки 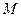от источников.

Рассмотрим два предельных случая:

1. Пусть разность 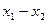равна целому числу длин волн, т.е.

,

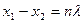где 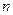- любое целое число.

Тогда 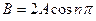. Т.к. 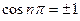, то

.

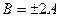Амплитуда результирующих колебаний удвоилась, по сравнению с амплитудами обоих колебаний.

2. Пусть разность 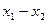равна нечетному числу полуволн, т.е.

.

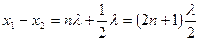Тогда 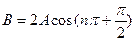. Т.к. , то

.

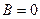Амплитуда результирующих колебаний равна нулю. Волны взаимно уничтожили друг друга.

Физическое объяснение этого явления следующее: если разность хода двух волн одинаковой амплитуды равна целому числу длин волн, то в точке 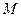обе волны одновременно вызовут одинаковое смещение – либо вверх – либо вниз. Если же разность хода отличается на целое нечетное число полуволн, то смещения, вызываемые волнами, одинаковы по величине, но противоположны по направлению. В таких точках волны гасят друг друга.

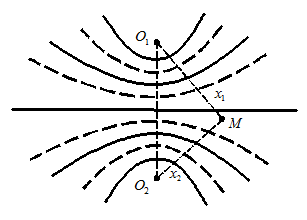
Как мы уже знаем из аналитической геометрии, геометрическое место точек, разность расстояний от которых до точек 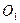и 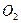равна постоянной величине, является гиперболой. Таким образом, геометрическое место точек, в которых колебания усиливают или ослабляют друг друга, представляют собой семейство гипербол (как мя и изобразили на рисунке). Сплошными линиями указаны места, в которых колебания усиливают друг друга, пунктирными – места, в которых колебания ослабляют друг друга.

Мы рассмотрели случай, когда амплитуды обоих колебаний одинаковы. В случае, если амплитуды 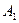и 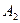различны, то в точках, где разность хода обоих колебаний равна целому числу волн, амплитуда результирующих колебаний равна .

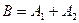В точках, где разность хода обоих колебаний равна целому нечетному числу полуволн, полного погашения не произойдет, но амплитуда достигает своего наименьшего значения, равного модулю разности амплитуд .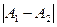

Интерференцию волн на графике используют для определения длины волны. Более подробно этот эксперимент мы рассмотрим в разделе «Оптика», когда будем изучать определение длины световой волны.

Принцип Гюйгенса. Дифракция волн.

Как мы уже знаем, упругие колебания передаются на большие расстояния не мгновенно, а постепенно – от одной точки среды к другой. Это обстоятельство лежит в основе принципа предложенного в конце 17 века голландским физикой Гюйгенсом, согласно которому каждая точка волнового поля, пришедшая в колебание, становится саамам источником вторичных волн.

Результирующая волна, распространяющаяся дальше, возникает вследствие наложения и интерференции всех волн от этих вторичных элементарных источников.

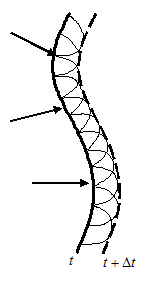С помощью принципа Гюйгенса можно найти вид фронта волны через малый промежуток времени 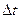. Для этого нужно из каждой точки фронта, являющейся вторичным источником волн, провести в направлении распространения сферическую волну радиуса 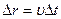, где - скорость распространения волн.

Новый фронт волны получается как огибающая этих вторичных волн. (В принципе, вторичные волны распространяются и в направлении, противоположном основной волне, однако волны бегущие назад, намного меньше, чем те же вторичные волны, бегущие вперед. Поэтому их величиной в дальнейшем пренебрегаем. Доказательство того, что вторичные волны не дают заметной волны, бегущей назад, было получено из строгой математической теории Кирхгофом. Мы ее в нашем курсе не рассматриваем.)

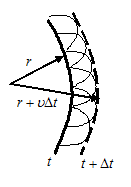
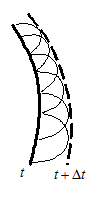
Применяя построение Гюйгенса для случая плоской волны, мы видим, что в однородной среде плоская волна при своем распространении остается плоской.

Аналогичными свойствами сохранения формы обладает и сферическая волна.

Принцип Гюйгенса применим и для волн, распространяющихся в неоднородной среде. В этом случае скорости распространения вторичных волн будут меняться от точки к точке и, соответственно, различными будут радиусы полусфер, проводимых из разных точек исходного фронта.

Огибающая этих волн дает новое положение фронта волны. На данном примере скорость волны в нижней части рисунка больше, чем в верхней.

Принцип Гюйгенса позволяет объяснить характерное для волнового движения явление непрямолинейного распространения волн, носящее название дифракции.

1. 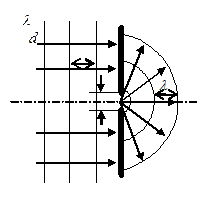Рассмотрим плоскую волну, падающую на поверхность экрана, в котором имеется отверстие, малое по сравнению с длиной волны (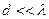). Когда фронт волны дойдет до экрана, вторичные источники, расположенные в плоскости отверстия, создадут расходящуюся от него сферическую волну за экраном. Это иллюстрирует принцип Гюйгенса, согласно которому отверстие на экране можно рассматривать, как одиночный элементарный источник (если ширина его ).

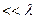2. При большом отверстии в экране с 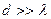имеем прямолинейное распространение волн за экраном. Это и есть результата интерференции за экраном волн от многих вторичных источников. Однако и в этом случае на боковых границах волнового фронта наблюдаются отклонения от прямолинейного распространения.

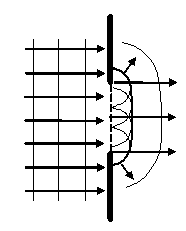Аналогично можно показать, что в результате дифракции за малой, по сравнению с длиной волны, преградой не образуется тени. Преграда соизмеримая с длиной волны сильно рассеивает волны, а преграда, размеры которой много больше длины волны, образует тень, хотя и здесь волны частично огибают препятствие, заходя в область геометрической тени.

Итак, волны всегда в большей или меньшей степени огибают препятствия, причем степень огибания зависит от величины препятствий по сравнению с длиной волны: чем меньше препятствие, тем отчетливее явление дифракции.

Отсюда определение: дифракция – это огибание волнами препятствий, соизмеримых с длиной волны.

Количественный расчет некоторых дифракционных явлений и их практические применения будут подробно рассмотрены в курсе «Оптики».

При помощи принципа Гюйгенса объясняется также закон отражения и преломления волн на границе раздела двух сред. Соответствующие построения для световых волн применимы и для упругих волн в механических средах.

Допустим, что на границу раздела двух однородных изотропных сред, в которых скорости распространения колебаний равны 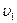и 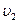, падает плоская волна 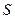. Нормаль к фронту этой волны составляет с нормалью к поверхности раздела этих сред угол (угол падения).

Пусть положение фронта падающей волны в момент времени 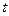будет равно 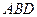. Определим положение фронта этой волны в момент времени 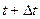. Для этого из точек 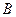и 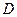опишем полусферы радиуса 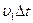. Их огибающая и даст нам фронт волны в первой среде в момент времени .

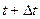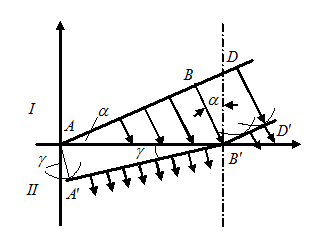Определим положение этого фронта во второй среде. Для этого из точки 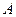, лежащей на поверхности раздела этих сред, опишем во второй среде полусферу радиуса 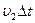. Для построения огибающей проведем из точки 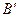касательную к этой полусфере 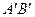. Это и будет фронт преломленной волны. Нормаль к фронту этой волны образует с нормалью к поверхности раздела двух сред угол 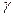(угол преломления).

Рассмотрим 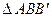: в нем (как углы с взаимно перпендикулярными сторонами), а 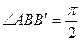. Тогда 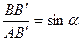. Т.к. 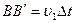, то .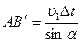

Аналогично, из .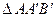

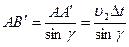Приравнивая эти равенства, получим

или 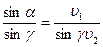- закон преломления.

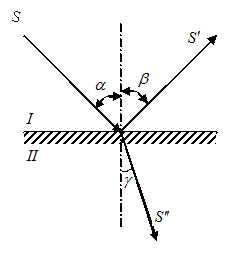
Подобным образом выведем закон отражения.

Построим, как и раньше, фронт падающей плоской волны 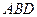в момент времени 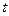и ее фронт 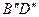в момент времени .

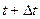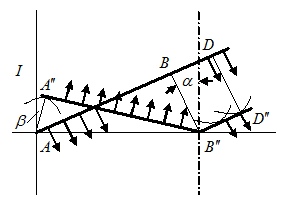Определим положение этого фронта после отражения. Для этого из точки 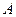в той же среде 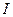опишем полусферу радиуса 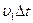. Для построения огибающей проведем из точки 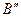касательную 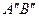к этой полусфере. Это и будет фронт отраженной волны. Нормаль к фронту этой волны образует с нормалью к поверхности раздела двух сред угол 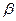(угол отражения).

Рассмотрим 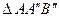и 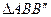. Эти треугольники равны, т.к. у них общая гипотенуза 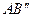и одинаковые катеты 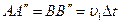. Следовательно,

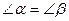- закон отражения.

Принцип консорционной целостности:

- -с исчезновением вида, образующего консорцию, исчезают и многие консорценты, не входящие в другие консорции или другие экосистемы («Никто не гибнет в одиночку»).

Принцип биологического замещения:

- вновь внедрившийся в экосистему вид, вырабатывая свою экологическую нишу, сужает возможности менее конкурентноспособных видов и тем самым ведёт к их вытеснению или исчезновению; видоизменяет экологические ниши близких по потребностям видов, создавая предпосылки для сокращения их численности или, наоборот, для массового размножения (поведение «незваного гостя»).

При этом меняется всё сообщество, включая формы, как будто и не связанные с внедрившимся видом. В результате смещается динамическое равновесие в системе и нарушаются внутренние и внешние связи.

Принцип смены трофических цепей:

– исчезнувшая или разрушенная трофическая сеть (или сеть) видов сменяется цепью видов – эколого-энергетических аналогов, что позволяет экосистеме усваивать и перерабатывать поступающую энергию, даже и с меньшей эффективностью («экосистема не терпит пустоты»).

Принцип неопределённости хозяйственного значения смены видов: – при замене трофических сетей вновь проникающие в систему или возникающие в ней виды могут быть как желательными, так и нежелательными в хозяйственном, медицинском, ветеринарном отношении («старый друг лучше новых двух»).

Это означает известную осторожность также при вселении и акклиматизации новых видов без продуманного биологического обоснования.

При организации особо охраняемых природных территорий важно применение закона обеднения разнородного живого вещества в островных сгущениях, предложенного Г.Ф.Хильми:

- индивидуальная система, действующая в среде с уровнем организации более низким, чем уровень самой системы, обречена – постепенно теряя свою структуру, система через некоторое время должна раствориться в окружающей среде.

Из этого закона вытекают два следствия:

1) для осуществления охраны исчезающих видов и редких биотических сообществ необходима достаточно обширная территория;

2) любые сложные биотические сообщества, сохранённые на незначительных пространствах, обречены на постепенную деградацию.

С расширением биоразнообразия в экосистемах может быть связан закон максимального использования энергии Г. и Ю.Одумов:

- в соперничестве с другими системами выживает и сохраняется та их них, которая наилучшим образом использует поступающую энергию, то есть преимущество имеют системы с максимальным КПД и минимумом рассеиваемой энергии.

С этой целью любая система:

- создаёт хранилища энергии с оптимальным режимом её использования, т.е. вариантами накопления и извлечения. В живых организмах подобные функции выполняют крахмал у растений, гликоген у беспозвоночных, АТФ у высших животных и человека;

- затрачивает накопленную энергию на обеспечение поступления новых порций энергии;

- создаёт механизмы регулирования, поддерживающие устойчивость системы и способность адаптации к изменяющимся условиям;

- налаживает с другими системами обмен, необходимый для обеспечения потребностей в энергии других типов.

Данная лекция составлена на основе материалов книги Н.Ф.Реймерса «Экология. Теории, законы, правила, принципы и гипотезы» (1994) и его же словаря-справочника «Природопользование» (1990).

Дата добавления: 2013-12-14