
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициенты аппроксимации
|
|
|
|
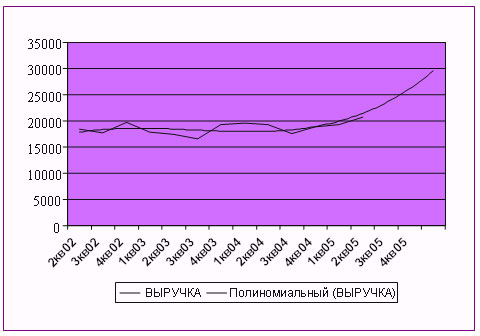
Рис. 4. – Динамика выручки и скользящая средняя выручки
Выручка, сглаженная методом скользящей средней (3-х линейный фильтр) подтверждает тезис и имеющейся положительной динамике. Тенденция динамики — объективно существующее явление, которое можно описать аналитически и отобразить в формализованном виде уравнением некоторой линии. Линия, наилучшим образом характеризующая обобщенную тенденцию называется трендом.
Полученная в результате сглаживания динамическая кривая может быть подвергнута выравниванию на базе определенного типа линии. Визуально определить тип линии, наилучшим образом описывающим динамику, не представляется возможным. Выявление типа линии может быть определено путем сравнения коэффициента аппроксимации.
Для выявления типа линии тренда были рассмотрены линейная, степенная, логарифмическая, экспоненциальная и полиномиальная функции различных степеней.
Полученные уравнения различных зависимостей по сглаженным данным имеют вид:
Линейная: y = 248,94x + 16879, R2 = 0,3627;
Логарифмическая: y = 1352,8Ln(x) + 16299, R2 = 0,2285;
Степенная: y = 16534x0,0678; R2 = 0,2241;
Экспоненциальная: y = 17021e0,0125x; R2 = 0,3557;
Полиномиальная второй степени: y = 55,731x2 - 698,49x + 20000,
R2 = 0,5953;
Полиномиальная третьей степени: y = 8,6412x3 - 164,62x2 + 923,46x + 16827, R2 = 0,6625
Самое высокое значение коэффициента аппроксимации имеет полиномиальное уравнение третьей степени (табл. 8).
| Таблица 8. |
| Вид уравнения | по фактическим данным | по выровненным данным |
| Линейное | 0,2135 | 0,3627 |
| Степенное | 0,1016 | 0,2241 |
| Логарифмическое | 0,1002 | 0,2285 |
| Экспоненциальное | 0,2012 | 0,3557 |
| Полином второй степени | 0,3898 | 0,5953 |
| Полином третьей степени | 0,4735 | 0,6625 |
Сравнение коэффициентов аппроксимации показывает, что наиболее высокая аппроксимация получена при построении полинома третьей степени (рис. 5), следовательно, именно это уравнение и может быть использовано при разработке стратегии в целях прогнозирования выручки при сохранении условий функционирования предприятия в перспективе.
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 5029; Нарушение авторских прав?; Мы поможем в написании вашей работы!