Бінарні відношення

Вступ

Моделювання переваг на множині альтернатив

Розглянемо задачі вибору в умовах визначеності. Для того, щоб мати можливість здійснити порівняння альтернативи із атрибутами з іншою альтернативою 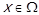, атрибути якої , згідно із деяким критерієм , в теорії прийняття рішень таке порівняння формалізується поняттям відношення переваги, яке дозволяє широко застосовувати апарат бінарних відношень. Використання відношення переваги аналогічне декомпозиції проблеми вибору альтернативного рішення з 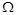на:

· розв’язання задачі попарного порівняння альтернатив;

· визначення принципу відбору на основі попарних порівнянь;

· вибору найкращих альтернативних рішень.

Слід зазначити, що застосування відношень переваги можливе лише для тих задач, в яких оцінка переваги між двома альтернативами 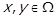не залежить від співвідношення цих альтернатив з рештою .

Моделювання переваг зустрічається в багатьох дисциплінах, наприклад:

· в економіці відношення переваги є частиною моделі «раціонального споживача»;

· в психології вивчаються судження про переваги, які збираються експериментально;

· в політології вивчається питання визначення колективної переваги на основі думок окремих виборців;

· в дослідженні операцій напрямок оптимізації цільової функції (максимізація або мінімізація) означає визначений напрямок переваги;

· в штучному інтелекті проектування поведінки автономних інтелектуальних агентів означає визначення для кожного з них що є бажаним, а що – ні.

Далі буде наведений опис властивостей бінарних відношень, що використовуються в теорії прийняття рішень. Слід зазначити, що характер об’єктів, на множині яких задається відношення, для подальшого викладення не є суттєвим.

Бінарним відношенням R на множині 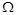називається множина впорядкованих пар . Множина 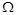називається областю визначення відношення R. Те, що деяка впорядкована пара 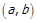належить відношенню 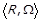(читається «a знаходиться у відношенні R з b»), записується як 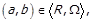або . Допускається спрощений запис 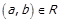або , якщо множина, на якій задано відношення, зрозуміла із контексту.

Щоб задати відношення R на множині 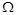, потрібно деяким чином вказати ті пари 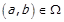, які належать R. Це можна виконати наступними способами.

1. Безпосередній перелік впорядкованих пар

.

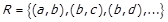2. Представлення графом.

Поставимо у взаємно однозначну відповідність елементам множини 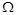вершини графа . Елемент 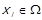та відповідну вершину графа будемо позначати однаково. Граф 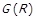відношення R містить дугу, що направлена від 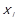до тоді й тільки тоді, коли виконується 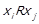. Матрицю суміжності 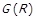будемо позначати , її будемо називати матрицею відношення R.

3. Представлення відношення за допомогою загальної властивості.

.

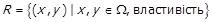Це представлення явно визначає відношення як множину впорядкованих пар.

4. Визначення за допомогою перерізів.

Верхнім перерізом відношення 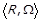для елементу x називається множина усіх елементів 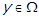, що знаходяться із елементом x у відношенні :

.

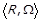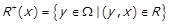Верхньому перерізу скінченного відношення відповідає стовпець його матриці.

Нижнім перерізом 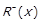відношення 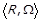для елементу x називається множина усіх елементів 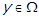, з якими елемент x знаходиться у відношенні R:

.

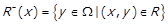Нижньому перерізу скінченного відношення відповідає рядок його матриці.

Перші два способи визначення придатні лише для відношень із скінченною областю визначення 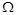, останні два способи придатні для визначення відношення і на нескінченній множині 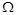. Введемо відношення спеціального вигляду.

Порожнім називається відношення, яке не виконується для жодної пари 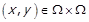. Як і порожня множина, таке відношення позначається символом .

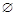Повним називається відношення, що виконується для усіх можливих пар , воно позначається як U.

Відношення називається діагональним (позначається E), якщо воно виконується для всіх , що складаються з однакових елементів, тобто 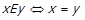. Граф містить лише дуги-петлі в усіх вершинах, і .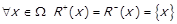

Дата добавления: 2013-12-14