Операції над бінарними відношеннями

Оскільки бінарні відношення являють собою множини, до них можна застосовувати класичні операції теорії множин. Так, для двох бінарних відношень 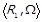та 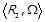визначаємо операції:

1) включення

;

2) доповнення

,
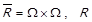або

;

твердження про те, що пара не належить відношенню R може за допомогою доповнення записуватись як 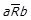; зазначимо, що відношення називається антидіагональним; для доповнення справедливі властивості де Моргана:

, ;

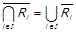3) перетину

;

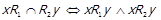4) об’єднання

.

Для двох бінарних відношень 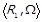та 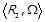додатково визначають операцію

5) композиції

.

Справедливі наступні властивості цієї операції (тут R також задано на Ω):

a. ;

b. ;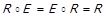

c. ;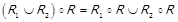

d. ;

e. в 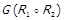присутні лише ті дуги, котрими можна замкнути направлений шлях довжиною 2, в якому перша дуга належить 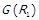, а друга – .

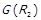Частковим випадком композиції відношень є квадрат відношення .

.

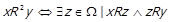За індукцією визначається n -й степінь відношення R:

.
Той факт, що , означає, що існує послідовність елементів 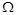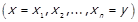така, що

.

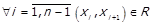Для бінарного відношення 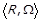додатково визначають такі операції:

6) обернення

;

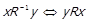очевидна властивість інволюції (інволютивності) обернення 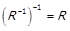, а також справедливі співвідношення для :

, ;
відносно композиції для обернення справедливо

;

7) транзитивного замикання, що позначається 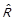, і

,
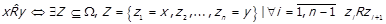тобто 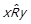тоді і тільки тоді, коли існує така послідовність елементів з підмножини 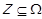, що складає направлений шлях в графі 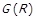, початком якого є x, а кінцем – y. За допомогою операції композиції транзитивне замикання можна виразити наступним чином:

;
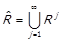справедлива рівність

;

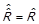8) редукції, що позначається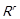

.
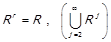Операція редукціє є зворотною до операції транзитивного замикання. З графу редукції відношення R виключаються усі дуги, що з’єднують початок та кінець якого-небудь направленого шляху довжиною більше 1 (рис. 1.1).

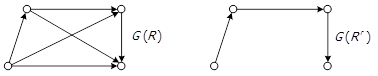
Рис. 1.1 – Приклад застосування операції редукції

Редукція має наступні властивості:

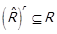a. ; b. ; c. .

Також слід зазначити операцію

9) звуження: відношення називається звуженням відношення 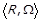на множину 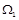, коли 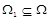, та ; звуження позначається 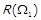. Граф 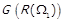є підграфом 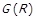, який породжено множиною вершин .

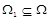Лема 1.1 .

Доведення. Нехай 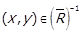, тоді 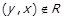. Припустимо, що 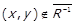. Тоді

.
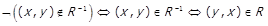Отримали протиріччя, тобто 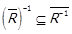. Аналогічно можна показати, що .

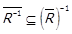Можна бачити, що у попередньому виведенні ми скористались аксіомою вибору. Цього можна уникнути, розглядаючи перерізи відповідних відношень. Крім цього, для скінченних відношень можна використати матричне представлення.

Наприклад, доведемо, що 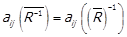. Маємо

,

.

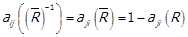Доведено.

Відношення називається двоїстим до відношення R.

Дата добавления: 2013-12-14