
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 11 Инерциальные навигационные системы
|
|
|
|
Инерциальные навигационные системы. Они занимают особое место благодаря особым уникальным возможностям, реализуемым при высокой степени помехозащищенности, скрытности и полной автономности выполнения полетного задания.
Принцип инерциальной навигации следует из классической механики И.Ньютона, положения которой справедливы без ограничений при решении задач приземной навигации. Базовой системой координат является инерциальная система координат, движущаяся прямолинейно и равномерно либо находящаяся в покое (абсолютная).

|
| Рис.2.9. Прецессия стоячей волны в волновом твердотельном гироскопе |
Инерциальный способ навигации заключается в вычислении вектора навигационных параметров (координат и скорости) ЛА путем решения в бортовой цифровой вычислительной машине системы дифференциальных уравнений, описывающих движение материальной точки под действием всех приложенных сил.
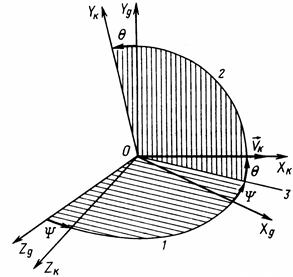 Рис.2.1 Взаимное расположение нормальной и траекторной систем координат (Ψ,θ)
Рис.2.1 Взаимное расположение нормальной и траекторной систем координат (Ψ,θ)
|  Рис.2.2 Взаимное расположение связанной и скоростной систем координат (α,β)
Рис.2.2 Взаимное расположение связанной и скоростной систем координат (α,β)
|
 = P cos α· cos β – Xa – mg sin θ =X;
= P cos α· cos β – Xa – mg sin θ =X;
 = P[ sin α· co sγa + cos α· sin β· sin γa]+Ya co sγa – Za sin γa – mg cos θ = Y;
= P[ sin α· co sγa + cos α· sin β· sin γa]+Ya co sγa – Za sin γa – mg cos θ = Y;
–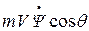 = P[sinα·sinγa – cosα·sinβ·cosγa]+ Ya sinγa + Za cosγa = Z (1.29)
= P[sinα·sinγa – cosα·sinβ·cosγa]+ Ya sinγa + Za cosγa = Z (1.29)
В связанных осях уравнения поступательного движения имеют следующий вид
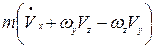 =
= 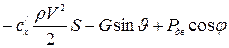
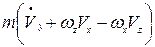 =
=  –
–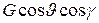 +
+ (1.30)
(1.30)
 =
= 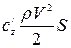 +
+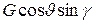 ,
,


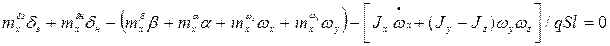

 (1.50)
(1.50)
 ,
,
Одновременно ИНС определяют вектор пилотажных параметров (углы курса, тангажа и крена), используемых при управлении пространственной ориентации ЛА, и вырабатывают сигналы, пропорциональные их производным, для системы автоматического управления полетом.
Источником первичной информации ИНС являются инерциальные измерители кажущегося ускорения (акселерометры) и абсолютной угловой скорости (ДУСы) либо ориентации ЛА (свободные гироскопы), объединенные в инерциальный измерительный блок (ИИБ). ИИБ и БЦМВ являются главными подсистемами ИНС.
Принципиальная схема инерциальной навигационной системы представлена на рис.2.10:  ,
,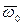 - векторы соответственно кажущегося ускорения и абсолютной угловой скорости ЛА, представленные проекциями на оси связанной с ним системы координат; БА и БГ – блоки акселерометров и гироскопов, поставляющие информацию, достаточную для приведения вектора кажущегося ускорения в базовую систему координат ИНС, в которой реализуется с помощью БЦВМ система основных уравнений навигации в параметрах абсолютной скорости
- векторы соответственно кажущегося ускорения и абсолютной угловой скорости ЛА, представленные проекциями на оси связанной с ним системы координат; БА и БГ – блоки акселерометров и гироскопов, поставляющие информацию, достаточную для приведения вектора кажущегося ускорения в базовую систему координат ИНС, в которой реализуется с помощью БЦВМ система основных уравнений навигации в параметрах абсолютной скорости 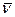 и геоцентрического вектора местоположения ЛА
и геоцентрического вектора местоположения ЛА  с использованием математической модели гравитационного поля Земли
с использованием математической модели гравитационного поля Земли 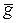 (
( ).
).
Принципиальные ограничения точности, присущие ИНС при идеальном ее воплощении, следуют из ее принципиальной схемы и определяются погрешностями начальных условий  , неадекватностью принятой математической модели реальному гравитационному полю Земли, а также характером поведения погрешностей ИНС.
, неадекватностью принятой математической модели реальному гравитационному полю Земли, а также характером поведения погрешностей ИНС.
Погрешности вертикального канала автономной ИНС (высоты и вертикальной скорости) измеряются по экспоненциальному закону и достигают неприемлемых значений за короткое время функционирования системы, в то время как навигационные погрешности в плане (погрешности координат и путевой скорости) изменяются по гармоническому закону с частотой, соответствующей частоте физического маятника с приведенной длиной, равной величине вектора 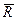 (частоте Шулера).
(частоте Шулера).
Варианты технической реализации ИНС определяются способом приведения измерений вектора кажущегося ускорения в базовую систему координат. Различают ИНС на базе гиростабилизированных платформ (ГСП), когда блок БА размещают на внутреннем элементе ГСП, физически реализующем базовую систему координат, и бесплатформенные ИНС (БИНС), в которых базовая систему координат реализуется аналитически.
ИНС-ГСП является сложным электромеханическим устройством прецизионного исполнения, стабилизация и управление ориентацией внутреннего узла которой осуществляются системой автоматического регулирования на основе показаний гироскопов. Преимуществами такого решения являются: ограниченные требования к измерениям гироскопов; улучшение условий работы акселерометров за счет изоляции их от угловых колебаний и вибраций корпуса ЛА; пониженные требования к БЦВМ.
К недостаткам ИНС-ГПС следует отнести их конструктивную сложность, высокую трудоемкость производства и существенные ограничения на тип измерительных элементов по массогабаритным и энергетическим характеристикам. В прецизионных ГСП трудно обеспечить маломагнитность конструкции, равножесткость и тепловую симметрию. Выполнение повышенных требований к надежности информационного обеспечения полета в ИНС-ГСП осуществляется резервированием систем и подсистем, что связано со значительными массогабаритными затратами.
БИНС лишены отмеченных недостатков. Возможность их реализации определяется достижениями цифровой вычислительной техники и решением проблемы динамического диапазона датчиков первичной информации (ДПИ) при достаточной точности измерения. БИНС отличаются: простотой конструкции ИИБ; возможностью повышения надежности ИИБ при наименьших совокупных затратах путем резервирования на уровне ДПИ; универсальностью применения, позволяющей использовать показания БИНС для информационного обеспечения задач навигации, пилотирования, а также наведения и управления бортовыми системами. БИНС легко адаптируются к специальным задачам применения, поскольку их модернизация осуществляется на уровне программного обеспечения. Стоимость современных БИНС составляет 1/2 стоимости ИНС-ГСП одинаковой точности.
Существенное увеличение числа решаемых БИНС задач, а также вычисление параметров ориентации в реальном масштабе времени предполагают более высокие по сравнению с ИНС-ГСП требования к производительности БЦВМ; при этом возрастают требования к качеству ДПИ по виброустойчивости и диапазону измерения.
Характерной особенностью алгоритмического обеспечения самолетных ИНС является вычисление скорости полета относительно земной поверхности. Основное уравнение навигации в этом случае записывается в системе координат (БСК), одна из осей которой совпадает с текущим положением вертикали места ЛА. Такое решение удобно для вычисления пилотажных параметров, облегчает начальную выставку и позволяет в ряде случаев обойтись без расходящегося вертикального канала ИНС, используя в алгоритме информацию о высоте и вертикальной скорости от радиовысотомера или системы навигации самолетных ИНС имеет вид:
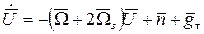 , (2.8)
, (2.8)

|
Рис.2.10. Принципиальная схема инерциальной навигационной системы:
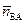 - вектор кажущегося ускорения, измеренный БА; - вектор кажущегося ускорения, измеренный БА;  - вектор абсолютной скорости, измеренный БГ; - вектор абсолютной скорости, измеренный БГ; 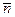 - вектор кажущегося ускорения, приведенный в инерциальную БСК - вектор кажущегося ускорения, приведенный в инерциальную БСК
|
где 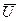 - вектор скорости ЛА относительно земной поверхности;
- вектор скорости ЛА относительно земной поверхности; 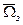 - вектор угловой скорости вращения Земли;
- вектор угловой скорости вращения Земли; 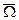 - угловая скорость базовой системы координат ИНС относительно земной поверхности, вычисляемая с использованием
- угловая скорость базовой системы координат ИНС относительно земной поверхности, вычисляемая с использованием 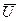 на основе представления о форме земной поверхности, аппроксимируемой референц эллипсоидом;
на основе представления о форме земной поверхности, аппроксимируемой референц эллипсоидом; 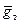 - вектор силы тяжести;
- вектор силы тяжести; 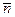 - вектор кажущегося ускорения, приведенный в сопровождающую БСК.
- вектор кажущегося ускорения, приведенный в сопровождающую БСК.
Таблица 2.2. Характерные требования к измерительным системам
| Параметр | Требования к БИНС | Требования к БИКВ |
| гироскопы | ||
| Диапазон измерения угловой скорости, °/с Систематический дрейф, °/ч Случайная погрешность, °/ч Погрешность масштабного коэффициента гироскопа, % Ассиметрия масштабного коэффициента, % Полоса пропускания скоростного гироскопа, Гц Квантизация выходного импульса, …" Погрешность съема свободного гироскопа, …" | 100…400 0,01 0,003 0,0005…0,005 0,0001 30…300 2…10 | 100…400 1,0…10,0 0,2 0,01…0,1 0,01 30…80 10…100 |
| акселерометры | ||
| Смещение нуля, мГал Погрешность масштабного коэффициента, % Погрешность юстировки, …" Время нагрева, мин Минимальный интервал между калибровками, год | 0,02 1…5 0,5 | 0,1 0,5…1,0 |
Решение ограниченного круга задач, например задачи информационного обеспечения пилотирования ЛА, осуществляется упрощенным вариантом ИНС – инерциальной курсовертикалью (ИКВ), которая отличается низкой стоимостью и использует более грубые измерительные элементы. Сравнение точностных требований к ИНС и ИКВ в бесплатформенном варианте их исполнения представлены в табл.2.2.
Системы навигации по физическим полям Земли. Один путь решения проблемы обеспечения требуемой точности ИНС заключается в совершенствовании инструментальных средств за счет повышения: точности акселерометров и гироскопов, однако этот подход связан с серьезными материальными затратами, что и результате приводит к низкой экономической эффективности предпринимаемых усилий.
Другой путь - использование недорогих ИНС, обладающих невысокими точностными характеристиками, в комплексе с дополнительными измерительными системами (барометрическими, радиолокационными, астрономическими, СНС и др.), которые позволяют осуществить коррекцию ИНС и, тем самым, повысить результирующую точность измерений. Однако применение астрономических систем ограничено метеоусловиями, радиолокационные системы снижают показатели помехозащищенности и автономности, барометрические системы могут привести к дополнительным погрешностям, порождаемым особенностями реальной атмосферы.
Задачи автономной навигации и коррекции ИНС в ряде случаев эффективно решают корреляционно-экстремальные навигационные системы (КЭНС), использующие естественные геофизические поля (ГФП), к которым относятся поле рельефа местности, магнитное» гравитационное, радиотепловое, оптическое и др. КЭНС являются обзорно-сравнительными навигационными системами.
На борту ЛА с помощью датчиков информации осуществляют текущие измерения поля, которые затем сравниваются с эталонными. Рассогласование текущих измеренных и эталонных значений геофизических полей, заложенных в память БЦВМ, используется при формировании соответствующего управления движением ЛА. Как правило, сопоставление эталонных и измеренных значений геофизических полей происходит посредством вычисления некоторого функционала типа корреляционной функции с последующим нахождением экстремума, что и определяет название таких систем.
В составе КЭНС могут использоваться ИНС-ГСП и БИНС, курсо-доплеровские, курсо-воздушные и другие системы. Часто КЭНС классифицируют по объему и характеру снимаемой информации; при этом выделяют точечные (одно измерение в конкретный момент времени), линейные и кадровые КЭНС. Такая классификация в известной степени условна и не является единственно возможной. Другой подход к классификации основан на различии типов используемых в них алгоритмов. Алгоритмическое обеспечение непрерывных беспоисковых КЭНС основано на использовании методов нелинейной теории следящих систем. Главные недостатки таких методов - потеря работоспособности системы при нестационарности геофизического поля по статистическим и спектральным характеристикам, расходимость при больших начальных отклонениях, превышающих радиус корреляции используемого поля.
Заметную роль в развитии КЭНС играют поисковые алгоритмы, основанные на теории статистических решений. В поисковых КЭНС сигналы от датчиков поля, записанные на некотором интервале времени, сопоставляются с рядом реализаций, каждая из которых соответствует определенной гипотезе об истинном движении ЛА на том же интервале времени, предшествующем текущему моменту. Поисковые алгоритмы КЭНС о принципе обеспечивают сходимость при больших начальных ошибках, однако реализация таких алгоритмов требует значительной производительности БЦВМ.
Дальнейшее развитие КЭНС привело к созданию оптимальных (субоптимальных) беспоисковых алгоритмов, основанных на методах теории фильтрации при наблюдении нерегулярного и не поддающегося аналитическому представлению геофизического поля. При этом удастся построить алгоритмы, удобные в вычислительном отношении.
На практике применяют также комбинированные алгоритмы, представляющие собой сочетание поисковых и беспоисковых алгоритмов. Как правило, они не имеют ограничений по начальным ошибкам рассогласования и часто не предъявляют жестких требовании к БЦВМ.
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 4532; Нарушение авторских прав?; Мы поможем в написании вашей работы!