
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В простейших линейных цепях
|
|
|
|
Анализ установившегося синусоидального режима
ЛЕКЦИЯ № 5
Учебные вопросы
1. Режимы работы последовательной RLC -цепи.
2. Расчетные соотношения в последовательной RLC -цепи. Треугольники напряжений и сопротивлений.
3. Режимы работы параллельной RLC -цепи.
4. Расчетные соотношения в параллельной RLC -цепи. Треугольники токов и проводимостей.
Литература: [1] с.122-137
1. Режимы работы последовательной RLC -цепи
При прохождении переменного тока через электрическую цепь, состоящую из последовательного соединенных резистивного, индуктивного и емкостного элементов (рис. 5.1) на зажимах этой цепи согласно второго закона Кирхгофа возникает напряжение, равное алгебраической сумме напряжений на отдельных элементах:
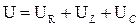 (4.1)
(4.1)

Рисунок 4.1 - Схема RLC -цепи
При этом напряжения на элементах цепи (UR, UL, UC) нужно рассматривать как составляющие приложенного к цепи напряжения U: собственно UR, UL, и UC – резистивная, индуктивная и емкостная составляющие этого напряжения. Согласно уравнениям связи напряжения и тока на резистивном, индуктивном и ёмкостном элементах эти составляющие при любом характере тока можно определить следующим образом:
 ;
; 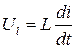 ;
;  .
.
С учетом последних соотношений уравнение (5.1) имеет вид:
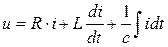 (4.2)
(4.2)
Это уравнение, называемое уравнением равновесия напряжений, лежит в основе исследования свойств последовательной RLC –цепи при любом характере тока, в том числе и при гармоническом токе.
Пусть последовательная RLC –цепь находится под гармоническим воздействием, тогда ее комплексная схема замещения имеет вид, изображенный на рисунке 4.2.

Рисунок 4.2 - Комплексная схема замещения RLC -цепи
Используя законы Ома и Кирхгофа в комплексной форме, представим уравнение равновесия напряжений (4.2) и всю систему уравнений электрического равновесия цепи в следующем виде:
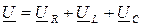 ;
;  ;
; 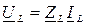 ;
;  (4.3)
(4.3)
 ,
,
где  ;
; 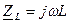 ;
; 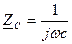 – комплексные сопротивления входящих в цепь идеализированных элементов.
– комплексные сопротивления входящих в цепь идеализированных элементов.
Решая систему (4.3) относительно тока I, получаем выражение закона Ома в комплексной форме для последовательной RLC–цепи:
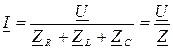 (4.4)
(4.4)
Комплексное входное сопротивление Z последовательной RLC –цепи равно сумме комплексных сопротивлений входящих в цепь элементов и определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия (рис. 4.2, б).
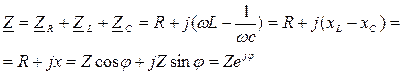 , (4.5)
, (4.5)
где 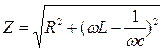 ,
, , (4.6)
, (4.6)
Z и φ - модуль и аргумент комплексного входного сопротивления.
Вещественная и мнимая части комплексного сопротивления представляют его активноеR и реактивное x сопротивления:
|
 ;
;
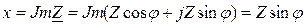
Анализ выражений (5.5) и (5.6) показывает, что характер входного сопротивления цепи зависит от состояния между индуктивным 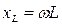 и емкостным
и емкостным 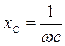 сопротивлениями. Здесь возможны три случая, которые иллюстрируются векторными диаграммами на рисунке 4.3
сопротивлениями. Здесь возможны три случая, которые иллюстрируются векторными диаграммами на рисунке 4.3

Рисунок 4.3 - Векторные диаграммы тока и напряжения
последовательной RLC -цепи
1. Если 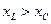 , т.е.
, т.е. 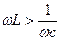 , следовательно,
, следовательно, 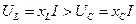 и
и 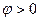 (рис. 4.3, а). Это означает следующее:
(рис. 4.3, а). Это означает следующее:
- напряжение опережает ток источника;
- цепь имеет индуктивный характер и работает в активно-индуктивном режиме.
2. При 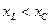 , т.е.
, т.е.  , выполняется соотношение
, выполняется соотношение 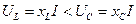 и
и 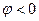 (рис. 4.3, б). Из этого вытекает следующее:
(рис. 4.3, б). Из этого вытекает следующее:
- напряжение отстает от тока источника;
- цепь имеет емкостной характер и работает в активно-емкостном режиме.
3. Если 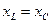 , то
, то 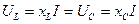 и
и  (рис. 4.3, в). Это означает следующее:
(рис. 4.3, в). Это означает следующее:
- напряжение на индуктивном и емкостном элементах полностью компенсируют друг друга, т.к. 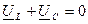 , а напряжение на резистивном элементе становится равным напряжению источника и совпадает по фазе с током (рис.5.3, в);
, а напряжение на резистивном элементе становится равным напряжению источника и совпадает по фазе с током (рис.5.3, в);
- сопротивление цепи имеет чисто резистивный характер иработает в режиме резонанса напряжений.
2. Расчетные соотношения в последовательной RLC -цепи. Треугольники напряжений и сопротивлений
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 2457; Нарушение авторских прав?; Мы поможем в написании вашей работы!