Треугольник сопротивлений

Треугольник напряжений

На рис.4.3,а,б,в приведены векторные диаграммы последовательной RLC- цепи для каждого из перечисленных установившихся режимов ее работы. Именно на основе таких диаграмм далее производится более детальный анализ свойств цепи и расчетных соотношений.

Из указанных векторных диаграмм цепи можно выделить треугольники напряжений, позволяющие записать расчетные соотношения для действующих или амплитудных значений всех напряжений в цепи. Такой треугольник напряжений для цепи, работающий в активно-индуктивном режиме, представлен на рис. 4.4, а, а в активно-емкостном режиме – на рис. 4.4, б.

Рис. 4.4 - Треугольники напряжений

Из треугольников напряжений видно, что любое синусоидальное напряжение на зажимах цепи можно разложить на активную и реактивную составляющие:

- активной составляющей напряжения будет является та, вектор которого совпадает по направлению с вектором тока;

- резистивной составляющей напряжения является составляющая, вектор которой нормален к вектору тока.

Из треугольников напряжений следует ряд расчетных формул для последовательной RLC – цепи:

; ;

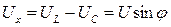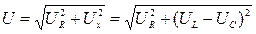; (4.8)

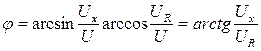
Таким образом, особенностью расчетных соотношений в цепях синусоидального тока для действующих значений величин является их запись на основе векторных диаграмм с учетом угла сдвига по фазе между ними.

От треугольника напряжений (рис. 4.4) путем деления длин его сторон на действующее значение тока I можно перейти к новому треугольнику, изображенному на рис. 4.5, а, б.

На основе формулы (4.3) и (4.5) можно записать:

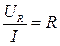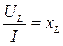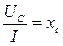; ; ; ; . (4.9)

Рис. 4.5 - Треугольник сопротивлений

С учетом этих обозначений получим треугольник (4.5, б), называемый треугольником сопротивлений данной цепи. Параметр Z называется полным сопротивлением цепи.

Из треугольника сопротивлений следует ряд новых расчетных формул:

; ;

;

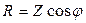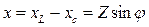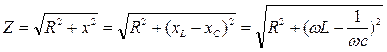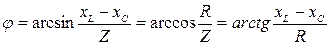. (4.10)

Полное сопротивление цепи Z – это еще один важный расчетный параметр цепи, не имеющий смысла для мгновенных значений тока (так же как 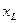и ), но обеспечивающий простую связь амплитуд или действующих значений тока и напряжения на зажимах цепи в форме закона Ома:

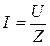; . (4.11)

3. Режимы работы параллельной RLC -цепи

Рассмотрим параллельную RLC -цепь (рис. 4.6, а), к зажимам которой приложено напряжение, изменяющееся по гармоническому закону. Мгновенные значения всех токов алгебраически суммируются на основе первого закона Кирхгофа:

I=I_R+I_L+I_C, (4.12)

где I_R=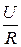=Ug - активная составляющая общего тока;

I_L=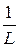 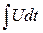- индуктивная составляющая общего тока;

I_C= C - емкостная составляющая общего тока.

Уравнение (4.1) можно представить в следующем виде:

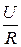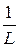
I =++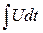C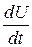; (4.13)

Комплексная схема замещения цепи, в которой идеализированные двухполюсные элементы представлены их комплексными проводимостями, изображена на рис. 4.6,б.

Рисунок 4.6 - Схемы параллельной RLC-цепи

Используя законы Ома и Кирхгофа в комплексной форме, составим систему уравнений электрического равновесия цепи:

I = I _R + I _L + I _L;

U = U _R = U _L = U _C (4.14)

I _R = Y _R U _R, I _L = Y _L U _L, I _C = Y _C U _C;

где Y _R = = g, Y _L = -j = - jb _L, Y _C = jω C = jb _C - комплексные проводимости соответственно резистивного, индуктивного и емкостного элементов.

Тогда уравнение (4.13) в комплексной форме примет вид:

I = g U + U + jC U = I _R + I _L + I _C; (4.15)

где I _R = g U - ток в сопротивлении (совпадает по фазе с напряжением);

I _L = 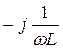U - ток в индуктивности (отстает от напряжения на π/2);

I _C = jC U - ток в емкости (опережает напряжение на π/2).

Решая систему уравнений (4.15) относительно тока I, получаем закон Ома в комплексной форме для параллельной RLC -цепи:

I = (Y _R + Y _L + Y _C) U = YU (4.16)

где Y = Y _R + Y _L + Y _C - комплексная проводимость RLC -цепи, равная сумме комплексных проводимостей входящих в цепь идеализированных элементов.

Комплексная схема замещения цепи, соответствующая выражению (5.16), приведена на рис.4.6, в. Используя уравнение (4.16), можно по заданному напряжению определить ток через внешние зажимы цепи и, наоборот, по заданному току вычислить приложенное к цепи напряжение.

Векторные диаграммы для токов и напряжения параллельной RLC -цепи приведены на рис.4.7

Комплексная проводимость параллельной RLC-цепи, как и комплексная проводимость любой линейной цепи, не зависит от амплитуды (действующего значения) и начальной фазы внешнего воздействия, а определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия:

Y = Y _R + Y _L + Y _C = g + j(b_C-b_L) = . (4.17)

Переходя от алгебраической формы к показательной:

Y = ye, (4.18)

Находим модуль y и аргумент υ комплексной проводимости RLC -цепи:

y ==.

υ = arctg = arctg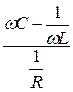. (4.19)

Анализ выражений (4.19) показывает, что характер проводимости, а, следовательно, и характер сопротивления цепи зависит от соотношения индуктивной и емкостной проводимостей.

Здесь можно рассмотреть три случая, которые иллюстрируются векторными диаграммами на рисунке 4.7.

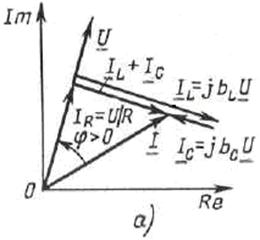
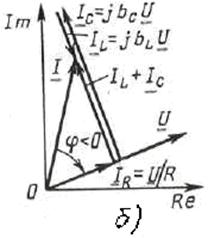
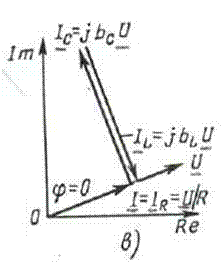
Рисунок 4.7 - Векторные диаграммы тока и напряжения

параллельной RLC -цепи

1. Если b _L > b _C, т.е. > C, то I_L = b_LU > I_C = b_CU и υ < 0, а φ > 0

Это означает следующее:

- напряжение определяет ток источника (рис.4.7,а);

- цепь имеет индуктивный характер;

- цепь работает в активно индуктивном режиме;

2. При b _L < b _C, т.е. <C, токи соответствуют I_L = b_LU < I_C = b_CU и υ > 0, а φ < 0.

Из этого вытекает следующее:

- напряжение отстает от тока (рис. 4.7, б);

- цепь имеет ёмкостный характер;

- цепь работает в активно емкостном режиме.

3. Если b _L = b _C, т.е. = C, то выполняется

I_L = b_LU = I_C = b_CU и φ = υ = 0. (4.20)

Это означает следующее:

- индуктивный и емкостной токи полностью компенсируют друг друга, т.к. I _L + I _C = 0, в результате чего ток через резистивный элемент равен току источника и совпадает по фазе с напряжением (рис.4.7,в);

- проводимость цепи имеет чисто резистивный характер;

- цепь работает в режиме резонанса токов.

Дата добавления: 2013-12-14