
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм расчета. Метод непосредственного применения законов Кирхгофа основан, как это следует из названия, на составлении системы уравнений по первому и второму законам
|
|
|
|
Содержание метода
МЕТОД НЕПОСРЕДСТВЕННОГО ПРИМЕНЕНИЯ ЗАКОНОВ КИРХГОФА
Метод непосредственного применения законов Кирхгофа основан, как это следует из названия, на составлении системы уравнений по первому и второму законам Кирхгофа и решении этой системы уравнений относительно искомых токов в ветвях заданной цепи. Условные положительные направления токов в ветвях, так же как и положительные направления обхода контуров, назначаются произвольно.
Уравнения по второму закону Кирхгофа составляются для независимых узлов, а по другому закону Кирхгофа - для независимых контуров цепи.
Узел цепи является независимым, если к нему присоединена хотя бы одна новая ветвь, не подходящая к ранее рассмотренным узлам.
Для цепи с q узлами независимыми узлами будет q-1 узел. Следовательно, по первому закону Кирхгофа может быть составлено число уравнений
M=q–1 (6.8)
Контур цепи является независимым, если он содержит хотя бы одну новую ветвь, не входящую в ранее рассмотренные контуры. Общее число N уравнений, которое может быть составлено по второму закону Кирхгофа, равно:
N=p-(q-1)=p–q+1, (6.9)
где p- число ветвей цепи.
Алгоритм расчета цепи методом непосредственного применения законов Кирхгофа предусматривает выполнение следующих этапов расчета:
1) составление исходной схемы замещения цепи;
2) перевод условий задачи в комплексную форму записи известных параметров цепи и электрических величин;
3) составление комплексной схемы замещения цепи и выбор условных положительных направлений токов в ветвях;
4) выбор независимых узлов и контуров и составление для них системы уравнений по первому и второму законам Кирхгофа;
5) решение системы уравнений относительно искомых комплексных токов и их оригиналов (мгновенных значений токов) и проверка правильности этого решения;
6) уточнение направлений найденных токов и проверка правильности решения задачи в целом. Проверка может быть осуществлена либо по законам Кирхгофа, либо на основе составления баланса комплексных мощностей.
Иллюстрация метода
Условия задачи. Для электрической цепи синусоидального тока, электрическая схема замещения которой изображена на рис. 6.3 определить токи в ветвях.

Рис.6.3 - Электрическая схема замещения цепи
Параметры элементов и функции ЭДС источников питания цепи заданы. Задачу решить методом непосредственного применения законов Кирхгофа.
Решение. Составляем комплексную схему замещения цепи; назначаем произвольно и указываем на схеме условные положительные направления комплексных токов (рис. 6.4).

Рис.6.4 - Комплексная схема замещения цепи
(метод непосредственного применения Кирхгофа)
Все заданные ЭДС и параметры выражаем в комплексной форме:
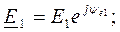

 Z 01
Z 01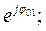
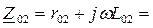 Z 02
Z 02
 Z 1
Z 1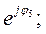

 Z 5
Z 5
 Z 6
Z 6
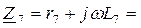 Z 7
Z 7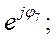
Выбираем независимые узлы и контуры и подсчитываем число уравнений, которое может быть составлено на основе первого и второго законов Кирхгофа. Всего должно быть составлено 6 уравнений (по числу неизвестных токов). Условные положительные направления обхода контуров выбираем также произвольно (в нашем примере по часовой стрелке).
По первому закону Кирхгофа число уравнений
M=q–1=4–1=3.
По второму закону Кирхгофа число уравнений
N=p+1–q=6+1–4=3.
Система уравнений имеет вид:
| Узел 1 | 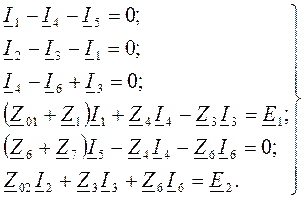 (6.9) (6.9)
|
| Узел 2 | |
| Узел 3 | |
| Левый контур | |
| Правый контур | |
| Нижний контур |
Решение полученной системы уравнений любым из известных методов позволяет определить комплексные токи. В частности, используя метод подставки, систему уравнений можно предварительно упростить, приведя к виду:
 (6.10)
(6.10)
Найденные комплексные токи (корни системы уравнений) должны быть подставлены в уравнения для проверки правильности решения системы уравнений. Должно получиться тождество - равенство левой и правой частей каждого уравнения.
По найденным комплексным токам на основе закона Ома можно определить комплексные напряжения на элементах.
Далее от комплексных токов и напряжений осуществляем переход к оригиналам - мгновенным или действующим значениям истинных токов в ветвях.
Проверка решения задачи в целом должна быть выполнена на этапе решения в комплексной форме (после нахождения всех комплексных токов и напряжений), либо на основе законов Кирхгофа для тех узлов и контуров, которые не входили еще в рассмотрение, либо по балансу комплексных мощностей, либо на основе построения векторной диаграммы цепи на комплексной плоскости.
При необходимости проверка может быть выполнена и на конечном этапе (для мгновенных значений токов и напряжений).
Достоинство метода - в его пригодности для расчета цепей любой сложности, недостаток - в громоздкости решения систем уравнений высоких порядков.
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 1381; Нарушение авторских прав?; Мы поможем в написании вашей работы!