Иллюстрация метода. Алгоритм расчета цепи синусоидального тока методом контурных токов предусматривает выполнение следующих основных этапов расчета:

Алгоритм расчета.

Алгоритм расчета цепи синусоидального тока методом контурных токов предусматривает выполнение следующих основных этапов расчета:

1) составление исходной схемы замещения цепи;

2) перевод условий задачи в комплексную форму записи;

3) составление комплексной схемы замещения цепи и выбор

независимых контуров;

4) выбор условных положительных направлений циркуляций комплексных контурных токов и составление системы контурных уравнений вида (6.11);

5) решение системы контурных уравнений относительно неизвестных комплексных контурных токов и проверку правильности решения системы уравнений;

6) определение комплексных токов в ветвях (по контурным токам) и запись оригиналов - реальных токов;

7) проверку правильности решения задачи в целом.

Условия задачи. Определить токи в сложной цепи, комплексная схема замещения которой представлена на рис.6.5. Комплексные ЭДС и параметры элементов заданы.

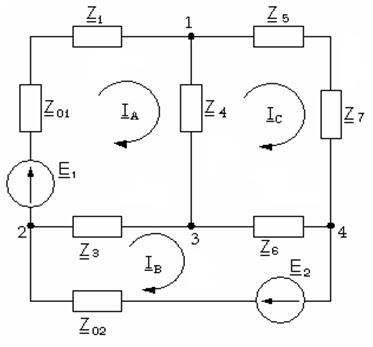
Рис.6.5 - Комплексная схема замещения цепи (метод контурных токов)

Решение. Произвольно выбираем направления циркуляции контурных токов в независимых контурах (рис.6.5.). Составляем систему контурных уравнений вида (6.11):

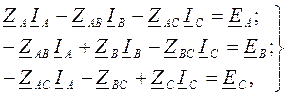(6.12)

где 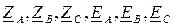- собственные комплексные сопротивления и собственные комплексные ЭДС выбранных контуров, соответственно, определяемые записанными ниже соотношениями:

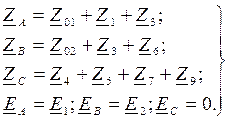(6.13)

В уравнениях (6.13) обозначены:

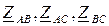- взаимные комплексные сопротивления ветвей, принадлежащих смежным контурам:

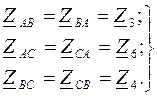(6.14)

Сопоставление системы уравнений (6.12) с учетом соотношений (6.13) и (6.14) с системой уравнений (6.10), относящейся к методу непосредственного применения законов Кирхгофа, свидетельствует об идентичности этих уравнений и служит обоснованием метода контурных токов.

Решение системы уравнений (6.12) относительно комплексных контурных токов с помощью определителей имеет вид:

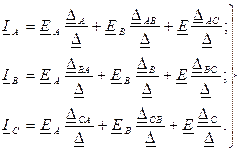(6.15)

где - главный комплексный определитель системы уравнений (6.12), а 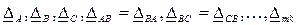- его алгебраические дополнения.

Главный определитель

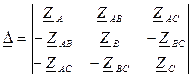(6.16)

Примечание. Алгебраическое дополнение (в общем случае) получается из главного определителя зачеркиванием m -ой строки и k -го столбца и умножением полученного определителя на .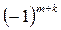

По найденным комплексным контурным токам (6.15) с учетом их направлений определяем значения и направления истинных комплексных токов в ветвях, которые аналогичны токораспределению, показанному на схеме рис. 7.5:

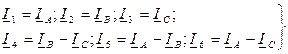(6.17)

Последние соотношения свидетельствуют о том, что первый закон Кирхгофа в методе контурных токов выполняется автоматически.

Выполнив необходимые проверки в комплексной форме, записываем оригиналы токов.

Дата добавления: 2013-12-14