Алгоритм расчета

Содержание метода

МЕТОД УЗЛОВЫХ НАПРЯЖЕНИЙ

Метод узловых напряжений (потенциалов) также предложен Максвеллом; его разработка, как и разработка метода контурных токов, была связана со стремлением уменьшить число уравнений при расчете сложной цепи.

Метод узловых потенциалов основан на первом законе Кирхгофа и законе Ома и предусматривает составление для заданной цепи, имеющей q узлов, системы так называемых узловых уравнений, состоящей из q-1 уравнения, и ее разрешение относительно неизвестных комплексных узловых напряжений, зная которые можно найти токи в цепи.

В данном методе комплексный потенциал одного из узлов цепи, называемый опорным узлом, принимается равным нулю.

Под узловыми напряжениями понимают напряжения остальных узлов цепи относительно опорного узла (напряжения ).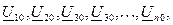

Узловое уравнение относительно какого-либо узла I записывается следующим образом:

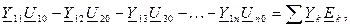(6.18)

где	-	собственная узловая комплексная проводимость узла I, определяемая как алгебраическая сумма комплексных проводимостей всех ветвей, присоединяющихся к узлу I;
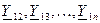	-	взаимные комплексные проводимости разветвления, определяемые как алгебраическая сумма комплексных проводимостей ветвей, соединяющих данный узел I с соответствующим индексу другим узлом цепи;
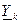	-	комплексная проводимость k -й ветви с источником ЭДС 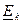, присоединенной к данному узлу I.

Необходимо помнить, что в уравнениях вида (8.1) стоящая справа сумма членов 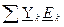является алгебраической. Перед произведением 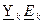ставится знак "плюс", если ЭДС направлена к узлу I, для которого составляется уравнение, и знак "минус", если ЭДС направлена от узла.

Обоснование уравнений вида (6.18) дано ниже при конкретной иллюстрации метода.

Алгоритм расчета цепи методом узловых потенциалов предусматривает выполнение следующих этапов расчета цепи:

1) составление исходной схемы замещения цепи;

2) перевод условий задачи в комплексную форму, составление комплексной схемы замещения и выбор опорного узла;

3) составление системы комплексных узловых уравнений вида (6.18);

4) решение системы узловых уравнений относительно комплексных узловых напряжений и проверка правильности решения этой системы;

5) определение комплексных токов в ветвях на основе закона Ома с учетом найденных узловых напряжений;

6) определение оригиналов - истинных токов в ветвях;

7) проверка правильности решения системы уравнений.

Дата добавления: 2013-12-14