Коэффициент связи

Индуктивная связь катушек.

Индуктивно связанные цепи

ЛЕКЦИЯ № 8

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ»

(ДГТУ)

Кафедра «Радиоэлектроника»

Руденко Н.В.

ЛЕКЦИЯ № 8

ИНДУКТИВНО СВЯЗАННЫЕ ЦЕПИ

по дисциплине ОСНОВЫ ТЕОРИИ ЦЕПЕЙ

Ростов-на-Дону
2013 г.

Учебные вопросы

1. Индуктивная связь катушек. Коэффициент связи.

2. Определение параметров катушек и коэффициента связи между ними.

3.Расчет цепей синусоидального тока с последовательно-соединенными и индуктивно-связанными катушками

Литература: [1] с.142-155.

В электротехнике и электронике широко используются устройства, которые содержат индуктивные катушки, связанные общими магнитными потоками. Примером такого устройства является трансформатор, который служит для преобразования уровней переменных напряжений и токов и для согласования сопротивлений отдельных участков цепи.

Физическая картина заключалась в следующем: переменный ток 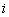, протекая по виткам катушки (рис. 8.1, а) создает переменный магнитный поток 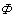, который сцепляясь с витками 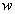катушки, обуславливает появление ЭДС самоиндукции e_L, противодействующей по закону Ленца изменению потокосцепления 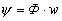, то есть

,

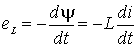где 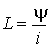- индуктивность, численно равная отношению потокосцепления самоиндукции к току, его обуславливающему.

Теперь рассмотрим явление взаимоиндукции, то есть явление наведения ЭДС в одной электрической цепи при изменении в ней потокосцепления, вызванного изменением тока в другой электрической цепи. Для этого проанализируем картину магнитного поля индуктивно-связанных катушек (рис. 8.1,б).

Рис.8.1 - К определению индуктивно связанных цепей

Связь магнитных потоков катушек обусловливает их индуктивную связь. Взаимно индуктивная связь проявляется в наведении ЭДС (называемой ЭДС взаимоиндукции) в одной катушке при изменении тока в другой близко расположенной катушке.

Цепи, в которых наводятся ЭДС взаимоиндукции, называют индуктивно связанными цепями.

Рассмотрим цепь, состоящую из двух индуктивных катушек, намотан-ных на общий сердечник (рисунок 8.2). На схеме обозначено: L ₁, R ₁ и L ₂, R ₂ – индуктивности и активные сопротивления первой и второй катушек; М – взаимная индуктивность.

Рисунок 8.2 ‑ Схема замещения двух, индуктивно связанных,

катушек

Взаимная индуктивность M зависит от индуктивностей обоих контуров и их взаимного расположения, поэтому при некоторой ориентации даже близко расположенных контуров взаимная индуктивность может быть равной нулю. Единица измерения взаимной индуктивности и индуктивности одинакова − генри.

Каждая из катушек пронизывается двумя магнитными потоками: потоком самоиндукции, вызванным собственным током, и потоком взаимоиндукции, вызванным током другой катушки.

В соответствии с принципом наложения потокосцепление первой катушки

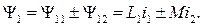(8.1)

Потокосцепление второй катушки

(8.2)

Значения взаимной индуктивности М в выражениях (8.1) и (8.2) одинаковы и не могут превышать среднего геометрического из значений и: L₁ и L₂:

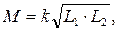
где k – коэффициент связи, характеризующий магнитную связь между катушками. Его величина равна отношению взаимной индуктивности и среднего геометрического значения индуктивностей обеих катушек:

где X_{L 1} и X_{L 2} – индуктивные сопротивления катушек.

В пределе, когда магнитный поток одной катушки полностью пронизывает витки другой, k =1. При отсутствии магнитной связи k =0.

Знаки слагаемых в (8.1) и (8.2) зависят от взаимного направления магнитных потоков катушек. В свою очередь, направления магнитных потоков зависят как от направления токов в катушках, так и от их взаимного расположения.

Если катушки включены таким образом, что потоки складываются, то такое включение называют согласным. Если магнитные потоки направлены навстречу друг другу, то катушки включены встречно.

При согласном направлении токов в двух индуктивно связанных ка-тушках зажимы этих катушек, относительно которых токи направлены одинаково, называют одноименными. Одноименные зажимы принято обозначать точками или звездочками.

Физически направления магнитных потоков в катушках определяется правилом правоходового винта. Например, потоки Ф_м1 и Ф_м2 на рис. 8.3,а направлены противоположно при заданных направлениях токов i ₁ и i ₂, т.е. катушки включены встречно. Однако, если бы эти токи были ориентированы одинаково относительно зажимов соответственно 1 и 4, то потоки были бы направлены одинаково. Следовательно, эти зажимы можно считать одноименными.

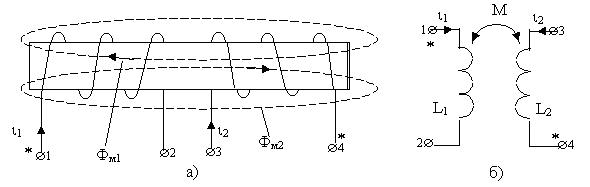
Рисунок 8.3 - Встречное включение катушек

На рис. 8.3,б изображена эл. схема, соответствующая рисунку 8.3,а, где

наличие индуктивной связи между катушками показано дугой с стрелками, над которой стоит символ "М", а одноименные зажимы помечены символами (*).

Определим напряжения на зажимах индуктивно связанных катушек на основе второго закона Кирхгофа:

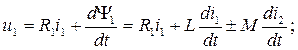(8.3)

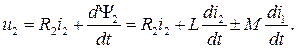(8.4)

Основной формой расчета цепей синусоидального тока является метод комплексных амплитуд. Рассмотрим применение этого метода для расчета индуктивно связанных цепей. Пусть цепь на рисунке 8.1 находится в режиме гармонических колебаний. Запишем уравнения (8.3), (8.4) в комплексной форме:

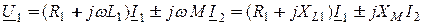; (8.5)

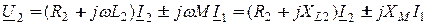, (8.6)

где 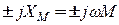- комплекс сопротивления взаимоиндукции; знак плюс (+ М) ставят при согласном включении катушек; знак минус (- М) - при их встречном включении.

Дата добавления: 2013-12-14