
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Асимптоты кривой
|
|
|
|
Пример.
Наибольшее и наименьшее значения функции на отрезке
Следует отличать минимумы и максимумы функций от наибольшего и наименьшего ее значений на заданном отрезке. Функция может не иметь экстремумов в исследуемой области, а наименьшее и наибольшее в этой области значения она имеет всегда.
Чтобы определить наибольшее и наименьшее значения функции на заданном отрезке, необходимо подсчитать значения функции в точках экстремума, входящих в исследуемую область, а также в граничных ее точках и выбрать среди них наименьшее и наибольшее значения.
Определить наибольшее и наименьшее значения функции  на отрезке
на отрезке 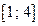 .
.
Находим точки, в которых производная обращается в нуль:
 , получаем две точки, одна из которых
, получаем две точки, одна из которых  не входит в исследуемую область, добавляем к ним граничные точки, тогда
не входит в исследуемую область, добавляем к ним граничные точки, тогда 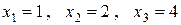 .
.
Определяем в этих точках значения функции  .
.
Таким образом, наименьшее в заданной области значение функции  реализуется при
реализуется при 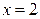 , наибольшее
, наибольшее 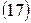 при
при 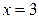 .
.
Задача о нахождении наибольшего и наименьшего значений функции одного вещественного переменного на отрезке с развитием компьютерных технологий перестает быть очень актуальной. С помощью программ MAXIMA мы можем легко построить график исследуемой функции и найти на нем все интересующие нас точки. Для того, чтобы построить график функции  на отрезке [1,4], следует ввести команду plot2d(x^3-3*x^2+1,[x,1,4]) и нажать Shift+Enter.
на отрезке [1,4], следует ввести команду plot2d(x^3-3*x^2+1,[x,1,4]) и нажать Shift+Enter.
graph.wxm
Определение. Прямая называется асимптотой кривой, если расстояние  от переменной точки M кривой до этой прямой при удалении точки M в бесконечность стремится к нулю.
от переменной точки M кривой до этой прямой при удалении точки M в бесконечность стремится к нулю.
На двух следующих рисунках асимптоты окрашены в красный цвет
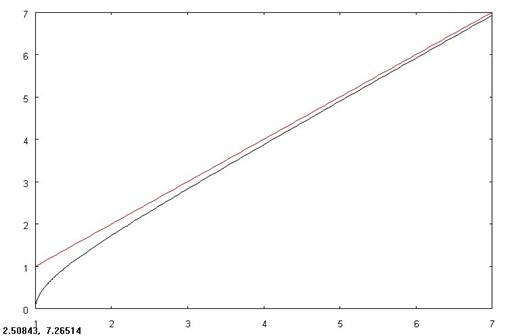
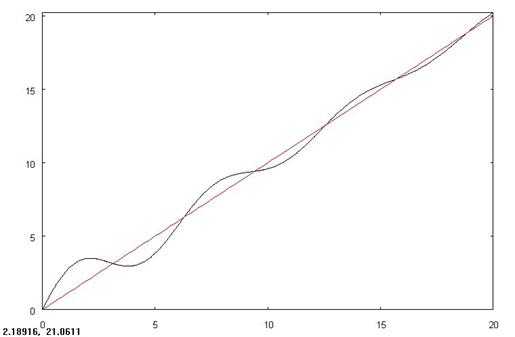
Асимптоты бывают вертикальными, они показывают поведение функции в окрестности особой точки, когда 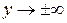 , и наклонными, дающими представление о поведении функции при
, и наклонными, дающими представление о поведении функции при 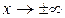 .
.
Если  особая точка, уравнение вертикальной асимптоты
особая точка, уравнение вертикальной асимптоты 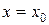 .
.
Теорема. Кривая  имеет наклонную асимптоту при
имеет наклонную асимптоту при  , уравнение которой
, уравнение которой 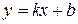 , если существуют пределы:
, если существуют пределы: 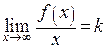 и
и 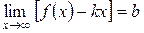 .
.
Доказательство. Из определения асимптоты следует 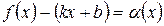 , где
, где  бесконечно малая при
бесконечно малая при  , то есть
, то есть 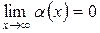 . Остается определить параметры уравнения асимптоты. Для этого вычислим
. Остается определить параметры уравнения асимптоты. Для этого вычислим 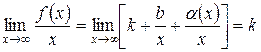 ,
, 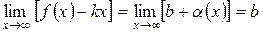 . Итак, если оба предела существуют и конечны, параметры прямой
. Итак, если оба предела существуют и конечны, параметры прямой  и
и 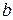 определены, причем точки этой прямой бесконечно сближаются с точками кривой при
определены, причем точки этой прямой бесконечно сближаются с точками кривой при  .
.
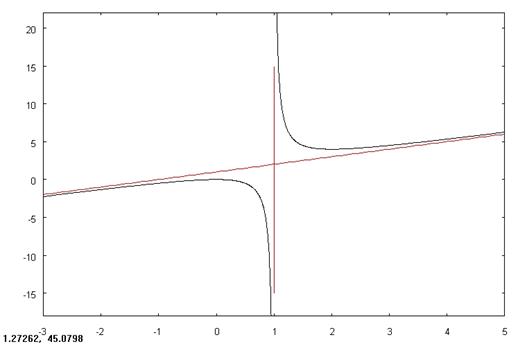
Пример. 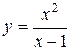 . Ясно, что
. Ясно, что 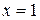 – уравнение вертикальной асимптоты.
– уравнение вертикальной асимптоты.
Определим  ,
,
 .
.
Наклонная асимптота при  имеет уравнение
имеет уравнение 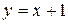 .
.
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 718; Нарушение авторских прав?; Мы поможем в написании вашей работы!