Основные уравнения для парциальных молярных величин

Парциальные молярные величины компонентов раствора взаимосвязаны. Так, если известна зависимость давления пара одного из компонентов бинарного раствора от его концентрации, то можно вычислить давление пара другого компонента. Это позволяет существенно сократить число экспериментальных определений, необходимых для термодинамической характеристики растворов.

Уравнения, связывающие парциальные молярные величины с составом раствора, носят названия уравнений Гиббса-Дюгема.

Так величина какого-либо свойства раствора равна:

где – парциальная молярная величина компонента, n₁, n₂ – число молей 1 -го, 2 -го и т.д. компонентов в растворе.

Или

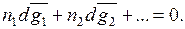
Если разделить это уравнение на 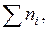получим соотношение, в которое входят мольные доли:

Разделив данное уравнение на 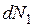при постоянстве р _общ, и T, получим уравнение

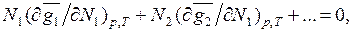
связывающее между собой парциальные молярные величины компонентов раствора.

Для бинарного раствора 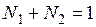и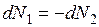

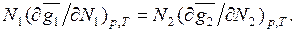(6.10)

Таким образом, если измерена величина как функция 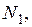то можно рассчитать Например,

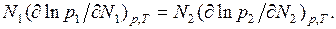(6.11)

Это важное уравнение связывает давление паров компонентов раствора и позволяет из измерений давлений пара одного компонента над раствором рассчитать давление пара второго компонента. Данное уравнение справедливо для любых растворов.

Зависимость парциальных молярных величин от концентрации могут иметь сложный характер. Например, на рис. 6.2 показана зависимость молярных объемов жидких сплавов магния и кадмия от состава. Изменение этих величин для одного моля сплава описывается кривой с максимумом и минимумом.

Пунктирная прямая, которая соединяет точку, соответствующую мольному объему чистого кадмия 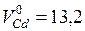см³/моль, с точкой для чистого магния 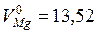см³/моль, отвечает идеальному случаю, когда при образовании раствора соблюдается аддитивность и при всех концентрациях 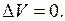Как видно из рис. 6.2, сплавы Cd – Mg, за исключением области до , образуются с уменьшением объема. Так для сплава см³/моль. Для этого сплава парциальные молярные объемы, определяемые по отрезкам на осях координат, отсекаемых касательной (штриховая линия А), составляют 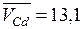см³/моль и см³/моль. Объем всего сплава близок к 12,65 см³/моль. В соответствии с уравнением (6.12) он должен составить см³/моль.

Рис. 6.2. – Молярные объемы жидких сплавов магния и кадмия

Дата добавления: 2013-12-13