Решение. Стержень переменного сечения с соотношением площадей поперечных сечений A1/A2 =2 находится под действием сосредоточенных сил и собственного веса (рис

Пример 24.

Пример 23.

Пример 22.

Стержень переменного сечения с соотношением площадей поперечных сечений A ₁/ A ₂ =2 находится под действием сосредоточенных сил и собственного веса (рис. а). Материал стержня на всех участках одинаков. Требуется построить эпюры распределения продольной силы и напряжений вдоль оси стержня и определить перемещение сечения а–а.

Решение.

Строим эпюры изменения продольной силы и напряжений вдоль оси стержня. Собственный вес стержня принято учитывать, заменяя его распределенной по всей длине нагрузкой. Интенсивность распределенной нагрузки равна собственному весу, действующему на единицу длины стержня, т. е.

на первом и втором участках

,

на третьем участке

,

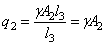где 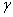– объемный вес материала стержня.

Эпюры продольной силы и напряжений строим, используя метод сечений. Заметим, что угол наклона эпюры продольной силы зависит от величины q и, следовательно, при построении эпюры N в масштабе угол ее наклона на первом и втором участке должен быть больше, чем на третьем участке, так как A ₁ по условию больше, чем A ₂ (рис. б). Угол же наклона эпюры напряжений зависит от объемного веса g, и поэтому угол наклона эпюры напряжений на всех участках одинаков (рис. в).

Находим перемещение (опускание) сечения а–а. Это перемещение можно искать разными способами. По первому способу для определения перемещения используем формулу 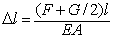. Здесь F – сосредоточенная сила, вызывающая перемещение участка длиной l; G – собственный вес рассматриваемого участка. Эту формулу можно использовать на участках постоянного сечения между сосредоточенными силами. Отсчет надо вести от неподвижного сечения, т.е. заделки. Например, в рассматриваемой задаче перемещение сечения а–а складывается из удлинения участка длиной l ₁, которое мы обозначим 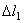, и удлинения участка длиной 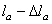. При определении удлинения 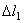в формуле сила F равна сумме F ₁, F ₂ и собственного веса всех расположенных ниже участков. Вес участка стержня длиной l ₁: 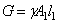. Таким образом, по формуле

.

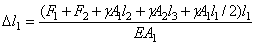Удлинение 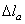происходит под действием сосредоточенной силы, состоящей из силы F ₂, веса участков стержня, расположенных ниже сечения а–а, и собственного веса участка 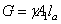. То есть

.

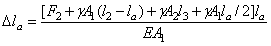Окончательно опускание сечения а – а равно .

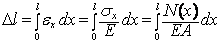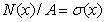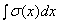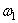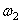Если построена эпюра распределения напряжений, то для определения перемещения заданного сечения удобно использовать второй способ, применяя формулу . В этой формуле , а – это площадь эпюры напряжений. Таким образом, если найти площадь двух трапеций на участке между неподвижным сечением (заделкой) и сечением а–а (заштрихованные площади и эпюры 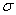на рис. в)и разделить полученную величину на модуль упругости, мы получим искомое перемещение сечения а–а:

.

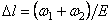При вычислении перемещения обращайте внимание на единицы измерения величин, входящих в формулы. Рекомендуем окончательный результат получить в сантиметрах.

Построить эпюры нормальных сил и нормальных напряжений для бруса, изображенного на рис. а. Принять a = 0,4 м; площадь поперечного сечения бруса на участках III и IV А = 20 см²; сосредоточенная сила F = 0,5 кН, собственный вес 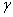= 0,0078 кг/см³ = 76,44 кН/м³.

Решение.

Для определения внутренних усилий разбиваем брус с прямолинейной осью на четыре участка. Проводим сечение I – I (рис. а) и отбрасываем верхнюю часть бруса, заменяя действие отброшенной части нормальной силой N ₁ (рис. б). Так как сечение I –I может быть проведено в любом месте участка I, то длина оставшейся части участка будет переменной величиной, и поэтому обозначим ее через x (рис. б), причем . Запишем уравнение равновесия, проектируя силы, действующие на оставшуюся часть бруса, на направление оси бруса:

а б в г д е ж

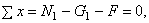откуда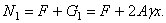

Через 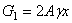обозначен собственный вес оставшейся части бруса первого участка, в пределах которого площадь поперечного сечения равна 2А, а длина оставшейся части обозначена через x. Подставим численные значения в полученную формулу:

.

Записанное выражение показывает, что эпюра нормальных сил в пределах первого участка представляет собой наклонную прямую линию. Для построения этой прямой определим значение нормальной силы N ₁ в начале первого участка (x = 0): N ₁(x = 0) = 500 Н и в конце первого участка (x = a= 0,5 м): N₁ (х = 0,5 м) =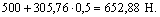

Полученные значения откладываем в масштабе в соответствующих точках эпюры нормальных сил (рис. е). Найденные точки соединяем прямой линией, затем штрихуем первый участок эпюры прямыми линиями, перпендикулярными к оси бруса.

Проводим сечение II – II и повторяем порядок расчета, описанный выше для сечения I – I. Переменная величина х участка II – II будет изменяться в пределах 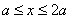. Составим уравнение равновесия (рис. в)

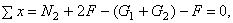откуда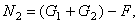

где 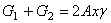– собственный вес части бруса, расположенного ниже сечения II – II.

Окончательно имеем

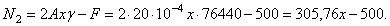
Определяем значение нормальной силы N ₂ в начале второго участка (х = 0,5 м):

и в конце этого же участка (х = х _max = 1 м):

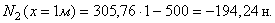
Полученные значения N ₂ откладываем в масштабе в начале и в конце второго участка (рис. е).

Проводим сечение III – III и для оставшейся части бруса составляем уравнение равновесия (рис. г)

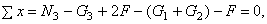
откуда где 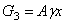– собственный вес оставшейся части бруса третьего участка; 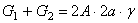– собственный вес первого и второго участков.

Тогда для участка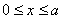

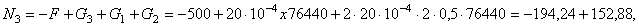
где нормальная сила N ₃в начале третьего участка будет N ₃(х =0) = – 194,2 Н; а в конце третьего участка получаем N ₃(х = a = 0,5 м) = – 117,8 Н. Найденные значения N ₃переносим на эпюру нормальных сил.

И наконец, рассматривая равновесие оставшейся части бруса, после проведения сечения IV – IV получаем (рис. д)

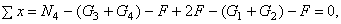
откуда 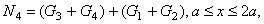где 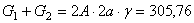Н– собственный вес участков I – I и II – II, 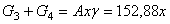– собственный вес третьего и оставшейся части четвертого участков.

В этом случае имеем

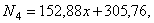
т.е. в начале четвертого участка N ₄(х = 0,5 м) = 382,2 Н, а в конце этого же участка N ₄(х = 1 м) = 458,64 Н. Вычисленные значения N ₄откладываем в масштабе на эпюре нормальных сил (рис. е).

Эпюра нормальных сил показывает, что первый и четвертый участок подвержены растяжению, а второй и третий – сжатию.

Для вычисления значений нормальных напряжений 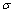и построения эпюры нормальных напряжений используем формулу:

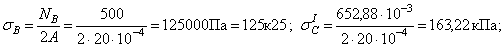
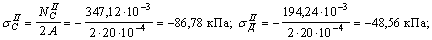
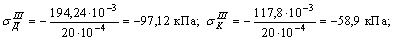
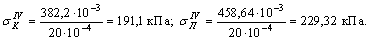
Эпюра нормальных напряжений показывает, что самое большое нормальное напряжение возникает в сечении, проходящем через точку Л четвертого участка (рис. ж), т.е. на опоре.

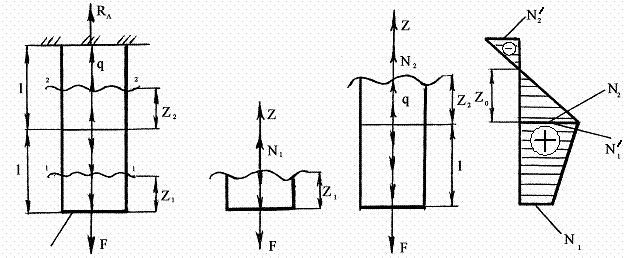
Дано: брус постоянной жёсткости (см. рис.) длиной 2 l, площадью поперечного сечения A, нагружен сосредоточенной силой F, распределённой нагрузкой интенсивностью q и собственным весом.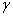

Требуется: построить эпюру N.

Эп N

1. Определение опорной реакции

Составим сумму проекций всех сил на продольную ось бруса Z:

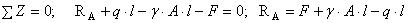
2. Установление силовых участков

Изучив действие внешних нагрузок F, 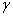, q на брус, нетрудно установить, что имеется два силовых участка:

- первый участок, 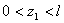, на котором N зависит от F и ;

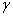- второй участок, 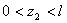, на внутреннюю силу N оказывают влияние F, 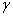, q.

3. Составление аналитических выражений для нормальной силы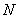

С учётом метода сечений брус рассекаем на две части, отбрасываем верхние отсечённые части, заменяя их действие силами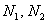. Целесообразно силы N₁ и N₂ направить по внешней нормали к сечению, то есть предполагать, что они вызывают растяжение бруса.

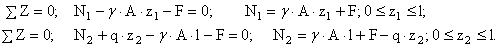
4. Вычисление значений N в характерных сечениях бруса

Определим значения N на границах силовых участков:

- при ;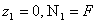

- при .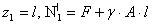

- при ;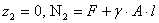

- при .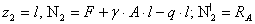

- при ;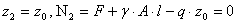

.

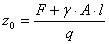По полученным результатам расчёта строим эпюру N с учётом масштаба (см. рис.).

Примечание. В расчётно-проектировочной работе необходимо результаты расчётов доводить до числовых величин. Для проверки правильности построения эпюры Nнужно воспользоваться следующими дифференциальными зависимостями:

.

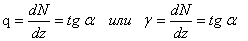Дата добавления: 2013-12-13