
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Из таблицы ГОСТа для уголка (рис
|
|
|
|
Пример 9.
Пример 8.
Пример 7.
Решение.
А) б) в)
Из таблицы ГОСТа для уголка (рис. а) находим
J 1=571 мм4, J 2=149 мм4, J 12=0, 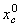 =3,45 мм,
=3,45 мм, 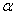 =-450, F =24,3 мм2.
=-450, F =24,3 мм2.
Центробежный момент
 мм4.
мм4.
Для уголка (рис. б) угол  ,
,
 мм4.
мм4.
Для уголка (рис. в) угол  ,
,
J xy=211 мм4.
Определить центробежный момент инерции неравнобокого уголка 160х100х10 относительно центральных осей, параллельных полкам (см. рис.).

Решение:
По таблице сортамента прокатной стали в соответствии с ГОСТ 8510-72 (СТ СЭВ 255-76) имеем  = 204 cм4,
= 204 cм4, 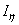 = 667 cм4, Iu min = 121 cм4,
= 667 cм4, Iu min = 121 cм4, 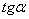 = 0,390.
= 0,390.
Для определения центробежного момента инерции  воспользуемся формулами поворота осей (переход от главных осей
воспользуемся формулами поворота осей (переход от главных осей 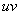 к данным
к данным 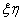 )
)
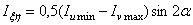 .
.
Угол в данном случае отрицателен, так как кратчайшее совмещение оси 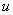 с
с  происходит по часовой стрелке. Главный момент инерции
происходит по часовой стрелке. Главный момент инерции 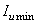 задан в таблице сортамента, а главный момент
задан в таблице сортамента, а главный момент 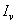 определяем из соотношения
определяем из соотношения
 ,
,
откуда  = 204 + 667 – 121 = 750 см4.
= 204 + 667 – 121 = 750 см4.
Таким образом, центробежный момент уголка будет равен
 = 0,5(121-750)×(-0,677) = 213 см4.
= 0,5(121-750)×(-0,677) = 213 см4.
Определить центробежный момент инерции равнобокого уголка 100х100х10 относительно центральных осей, параллельных полкам (см. рис.).

Решение:
По таблице сортамента прокатной стали в соответствии с ГОСТ 8509-72 (СТ СЭВ 104-74) имеем 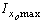 =284 см4,
=284 см4,  =74,1 см4,
=74,1 см4,  =3,84 см,
=3,84 см, 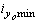 =1,96 см.
=1,96 см.
Пользуясь формулой поворота, находим
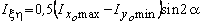 ,
,
 см4.
см4.
Определить центр тяжести треугольного поперечного сечения, показанного на рисунке.




Поперечное сечение представляет собой равнобедренный треугольник, а следовательно, ось у – ось симметрии и центр тяжести рассматриваемого поперечного сечения лежит на этой оси.
Для нахождения центра тяжести используем формулу  Запишем
Запишем
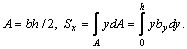 (а)
(а)
Из подобия треугольников 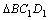 и
и 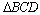 находим
находим
 или
или 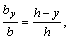 откуда
откуда 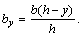
Найденное значение by подставляем в формулу (а) для вычисления статического момента Sx:
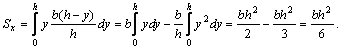
В этом случае формула  дает
дает

На рисунке проводим линию у = ус = h/ 3. Центр тяжести треугольного поперечного сечения будет лежать на пересечении проведенной линии и оси у. Координаты центра тяжести этого сечения: х = 0, у = h/ 3.
Ответ: xc = 0, yc = 4 R/( 3 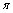 ).
).
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1222; Нарушение авторских прав?; Мы поможем в написании вашей работы!