Расчет предела выносливости материала при симметричном цикле напряжений

Расчетные методы оценки характеристик сопротивления усталости материалов и конструкций (детерминированный подход)

Рис. 1.7. Диаграмма предельных амплитуд цикла.

Рис. 1.5. Схематизированные кривые усталости для сталей.

Схематизированные кривые усталости для сталей

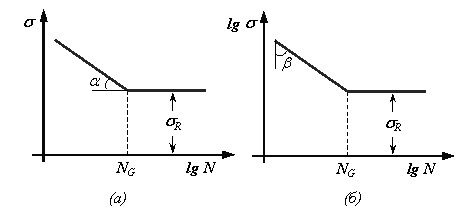
Левая ветвь кривой усталости на рис. 1.5, а соответствует уравнению Велера (1.1), где , а на рис. 1.5, б – уравнению Басквина (1.2), которое чаще в технической и учебной литературе представляют в ви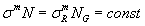де

, где 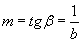. (1.7)

Абсцисса точки перелома схематизированной кривой усталости N_G (рис. 1.5, а, б) обычно принимает значения в диапазоне циклов.

Предел ограниченной выносливости , - максимальное по абсолютному значению напряжение цикла, соответствующее задаваемой циклической долговечности N. Пределы ограниченной выносливости выражаются в номинальных напряжениях.

Предел выносливости 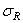, 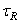- максимальное по абсолютному значению напряжение цикла, при котором не происходит усталостное разрушение до 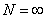; выражается в номинальных напряжениях.

Предел выносливости при симметричном цикле 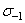, 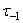- определяется по результатам испытаний на усталость при симметричном цикле напряжений, для которого ; .

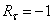Предел выносливости при отнулевом цикле напряжений 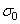, 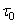- определяется по результатам испытаний на усталость при отнулевом цикле напряжений, для которого ; .

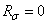Предельные напряжения цикла , , , 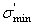- максимальное и минимальное напряжения цикла, соответствующие пределу выносливости, ; .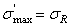

Предельная амплитуда и предельное среднее напряжение, соответствующие пределу выносливости,

; ;

; .

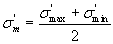Диаграмма предельных напряжений цикла – график, характеризующий зависимость между значениями предельных напряжений и значениями средних напряжений цикла для заданной долговечности (рис.1.6).

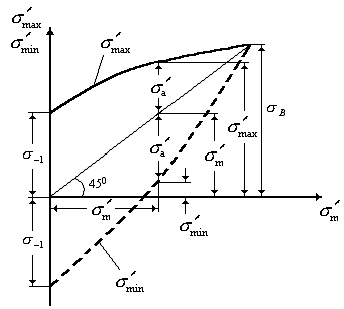
Рис. 1.6. Диаграмма предельных напряжений цикла: сплошная линия — , штриховая —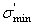

Диаграмма предельных амплитуд цикла – график, характеризующий зависимость между значениями предельных амплитуд и значениями средних напряжений цикла для заданной долговечности (рис.1.7.)

В качестве уравнения диаграммы предельных амплитуд на практике используются:

Уравнение Гудмана

, (1.8)

Уравнение Гербера

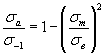, (1.9)

Уравнение И.А.Одинга

(1.10)

Уравнение Петерсона

(1.11)

УравнениеИ.А. Биргера

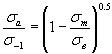(1.12)

Уравнение М.Н. Степнова

(1.13)

и другие.

Концентрация напряжений — повышение напряжений в местах изменения формы или нарушения сплошности материала (рис.1.8).

Надрез – резкие изменения размеров и формы объекта, вызывающее концентрацию напряжений (рис.1.8).

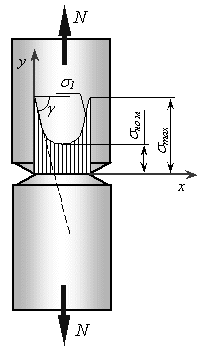
Рис. 1.8. Эпюра номинальных и первого главного напряжения в зоне надреза.

Номинальное напряжение — напряжение, вычисляемое по формулам сопротивления материалов без учёта концентрации напряжений, остаточных напряжений и упругопластического перераспределения напряжений в процессе деформирования,

, , .

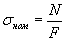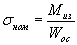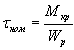Теоретический коэффициент концентрации напряжений – характеристика концентрации напряжений при упругом деформировании ,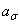

, .

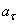
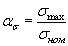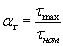Градиент первого главного напряжения — или (см. рис.1.8.)

Относительный градиент первого главного напряжения — .

Градиент касательного напряжения — скорость изменения касательного напряжения по направлению Х.

Относительный градиент касательного напряжения — .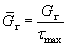

Эффективный коэффициент концентрации напряжений , — отношение предела выносливости образцов без концентрации напряжений к пределу выносливости образцов с концентрацией напряжений, имеющих такие же абсолютные размеры сечения, как и гладкие образцы,

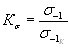, при .

Пределы выносливости с концентрацией напряжени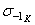й и 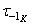выражаются в номинальных напряжениях.

Коэффициент чувствительности к концентрации напряжений 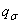, 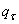- величина, определяемая по формуле

или .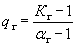

Коэффициент влияния абсолютных размеров поперечного сечения , — отношение предела выносливости гладких образцов диаметром d к пределу выносливости гладких лабораторных образцов d ₀=7,5-10 мм,

; .

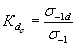Коэффициент влияния шероховатости поверхности K _F — отношение предела выносливости образцов с данной шероховатостью поверхности к пределу выносливости образцов с поверхностью не грубее R _a=0.32,

; .

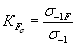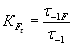Коэффициент влияния поверхностного упрочнения , 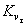— отношение предела выносливости упрочненных образцов к пределу выносливости не упрочненных образцов,

; .

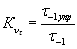Коэффициент снижения предела выносливости K — отношение предела выносливости стандартных гладких образцов к пределу выносливости объекта при симметричном цикле напряжений,

; .

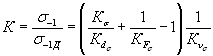Коэффициент чувствительности к асимметрии цикла напряжений 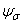, 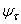— величина, определяемая по формулам

, .

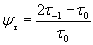Длительность и высокая стоимость испытаний на усталость побудили появление косвенных методов оценки предела выносливости материала, базирующихся на результатах статических испытаний материала и применении корреляционного и регрессионного анализа опытных данных.

Как показали результаты многочисленных исследований отечественных и зарубежных ученых, предел выносливости имеет тесную корреляционную связь с пределом прочности (временным сопротивлением) при статическом нагружении. На начальной стадии изучения сопротивления усталости материала предел выносливости сталей выражали как некую долю предела прочности,

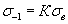(2.1)

В капитальной монографии английского ученого Р.Хейвуда [3], например, принято, что отношение предела выносливости при симметричном растяжении-сжатии к пределу прочности сталей, равно K =0,5. С учетом этого отношения им были разработаны методы оценки прочности деталей и элементов конструкций, обеспечивающие для того времени достаточную надежность инженерных решений.

Среди отечественных ученых наиболее серьезные исследования связей между усталостными и статическими характеристиками сталей выполнил С.Л.Жуков, который в послевоенные годы (1945 - 1947 гг.) опубликовал серию статей, посвященную этой проблеме.

В качестве основного уравнения линии регрессии С.Л.Жуковым и целым рядом других последователей использовалось линейное уравнение вида

(2.2)

В ряде работ использовались линейные уравнения двумерной и многомерной регрессии, связывающие предел выносливости сталей с характеристиками прочности и пластичности.

Ниже для примера приведены наиболее характерные уравнения, предложенные рядом авторов, для оценки предела выносливости при симметричном изгибе с вращением,

(С.Л.Жуков)

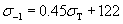(С.Л.Жуков)

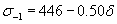(С.Л.Жуков)

(С.Л.Жуков)

(С.Л.Жуков)

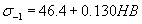(В.М.Гребеник)

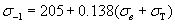(С.Л.Жуков)

(М.П.Марковец)

(В.М.Гребеник)

Все эти уравнения, а также уравнения (2.1) и (2.2), имеют два серьезных недостатка. Во-первых, в работах указанных и других авторов рассматривается лишь линейный характер связи между механическими характеристиками и без какого-либо обоснования игнорируется нелинейная зависимость, которая, как показывает регрессионный анализ [4], более адекватна опытным данным. Во-вторых, из-за относительно ограниченного объема статистического материала в этих работах недостаточно внимания уделено надежному обоснованию средней квадратической ошибки оценивания предела выносливости и её зависимости от уровня прочности материала, что не позволяет оценивать нижние (гарантированные) значения 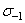материалов различной прочности.

Дата добавления: 2013-12-13